 por Fernandobertolaccini » Sex Jan 23, 2015 11:44
por Fernandobertolaccini » Sex Jan 23, 2015 11:44
Calcular
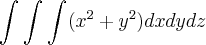
onde os limites de integração são:
![-R\leq x \leq R ; -\sqrt[]{R^2-x^2} \leq y \leq \sqrt[]{R^2-x^2}; 0 \leq z \leq \sqrt[]{R^2-x^2-y^2} -R\leq x \leq R ; -\sqrt[]{R^2-x^2} \leq y \leq \sqrt[]{R^2-x^2}; 0 \leq z \leq \sqrt[]{R^2-x^2-y^2}](/latexrender/pictures/f0238e3315137df46fe75331df7aba40.png)
Obs: tem que passar para coordenadas esféricas.
Resp: 4piR^5/15
Minha resposta deu 16piR^2/15, queria a resolução para saber no que errei
Obrigado !
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Ter Jan 27, 2015 20:16
por adauto martins » Ter Jan 27, 2015 20:16
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo do volume da esfera (coordenadas esféricas)]
por Horus123 » Qua Out 19, 2016 14:56
- 0 Respostas
- 4946 Exibições
- Última mensagem por Horus123

Qua Out 19, 2016 14:56
Cálculo: Limites, Derivadas e Integrais
-
- Coordenadas esféricas
por manuoliveira » Seg Jun 17, 2013 10:18
- 0 Respostas
- 1455 Exibições
- Última mensagem por manuoliveira

Seg Jun 17, 2013 10:18
Cálculo: Limites, Derivadas e Integrais
-
- Coordenadas esféricas
por Marcos_Mecatronica » Seg Jul 08, 2013 01:36
- 1 Respostas
- 1540 Exibições
- Última mensagem por young_jedi

Sex Jul 26, 2013 21:13
Geometria Analítica
-
- Sistemas de coordenadas esfericas
 por Jumarp » Sex Fev 25, 2011 22:58
por Jumarp » Sex Fev 25, 2011 22:58
- 4 Respostas
- 3114 Exibições
- Última mensagem por Jumarp

Dom Fev 27, 2011 12:37
Trigonometria
-
- Integral em coordenadas esféricas
 por bruna106 » Sáb Abr 09, 2011 15:22
por bruna106 » Sáb Abr 09, 2011 15:22
- 1 Respostas
- 2709 Exibições
- Última mensagem por LuizAquino

Seg Abr 11, 2011 11:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
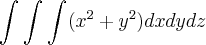 onde os limites de integração são:
onde os limites de integração são:![-R\leq x \leq R ; -\sqrt[]{R^2-x^2} \leq y \leq \sqrt[]{R^2-x^2}; 0 \leq z \leq \sqrt[]{R^2-x^2-y^2} -R\leq x \leq R ; -\sqrt[]{R^2-x^2} \leq y \leq \sqrt[]{R^2-x^2}; 0 \leq z \leq \sqrt[]{R^2-x^2-y^2}](/latexrender/pictures/f0238e3315137df46fe75331df7aba40.png)

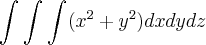 onde os limites de integração são:
onde os limites de integração são:![-R\leq x \leq R ; -\sqrt[]{R^2-x^2} \leq y \leq \sqrt[]{R^2-x^2}; 0 \leq z \leq \sqrt[]{R^2-x^2-y^2} -R\leq x \leq R ; -\sqrt[]{R^2-x^2} \leq y \leq \sqrt[]{R^2-x^2}; 0 \leq z \leq \sqrt[]{R^2-x^2-y^2}](/latexrender/pictures/f0238e3315137df46fe75331df7aba40.png)

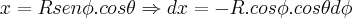
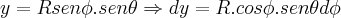
 ...
...![R\succeq 0,\phi\in[0,\pi],\theta\in [0,2\pi] R\succeq 0,\phi\in[0,\pi],\theta\in [0,2\pi]](/latexrender/pictures/0ce57871b6a413c8c5862eefe15bda0d.png) ...
...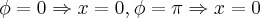
 ...
...
 ...ai meu amigo eh calcular em relaçao a
...ai meu amigo eh calcular em relaçao a  ,e depois em relaçao a
,e depois em relaçao a  ,analogamente q. foi feito em
,analogamente q. foi feito em 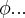

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
