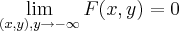por Fabio Wanderley » Sáb Dez 06, 2014 14:51
por Fabio Wanderley » Sáb Dez 06, 2014 14:51
Boa tarde!
Alguém poderia mostrar como se chegou a essa igualdade? Não a entendi. É uma passagem de um exercício de funções de duas variáveis aleatórias.
![\int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx \int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx](/latexrender/pictures/eaeeab1ab797ff823bcd4fccb45baf44.png)
Obrigado!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por Fabio Wanderley » Ter Dez 09, 2014 21:45
por Fabio Wanderley » Ter Dez 09, 2014 21:45
Consegui falar com um professor. Vou deixar aqui a explicação:
"A igualdade é verdadeira devido ao Teorema Fundamental do Cálculo. Quando se deriva uma integral e a variável de derivação é o limite superior da integral, o resultado é o integrando avaliado nesse ponto."
Depois revisei o conteúdo num livro de Cálculo I. Posto aqui em simbologia matemática a explicação do professor:
Teorema Fundamental do Cálculo:
Seja f contínua em [a,b] e
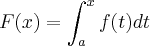
. Então F é derivável e F'(x) = f(x).
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por adauto martins » Qua Dez 10, 2014 14:51
por adauto martins » Qua Dez 10, 2014 14:51
meu caro fabio,
o q. esta dificultando aqui e o limite inferior da prim. integral...

,pois podemos fazer como se segue:
I=

,regra de leibinitz...
![I=\int_{-\infty}^{z-x}\partial F(x,y)=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty) I=\int_{-\infty}^{z-x}\partial F(x,y)=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty)](/latexrender/pictures/96ce2e4b496bf5c88bc5bc1d418fd5db.png)
,sem uma definiçao de F(x,y) nada podemos concluir com
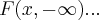
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Fabio Wanderley » Qua Dez 10, 2014 20:31
por Fabio Wanderley » Qua Dez 10, 2014 20:31
Adauto, pelo que entendi, você está utilizando a seguinte explicação do teorema fundamental do cálculo:
Se G é tal que G'(x) = f(x) para
![x\in\left[a, \right b] x\in\left[a, \right b]](/latexrender/pictures/18ec34837b9a94e30aab70ad4a837bda.png)
, então

Observe que o integrando e o intervalo de integração são diferentes da definição que usei.
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por adauto martins » Qua Dez 10, 2014 21:28
por adauto martins » Qua Dez 10, 2014 21:28
ai meu caro fabio,
claro tbem,nao tem como nao usar o teorema fundamental do calculo,mas ai usei a regra de leibnitz,mas cometi um erro ai,por displicencia(de sempre!)...
a regra de lebnitz p/funçoes de 2 variaveis eh:
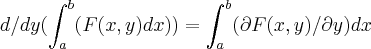
,desde de q. F(x,y)seja continua e diferenciavel em (a,b)...qto ao exercicio e o erro...
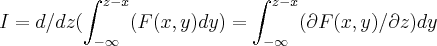
,meu erro foi

,mas persiste o problema do limite p/

vamos a exposiçao...z=u(x,y) continua e diferencial em (a,b)...logo


,
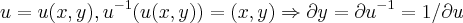

![I=\int_{u(-\infty}^{z-x}(\partial F).(\partial y/\partial u)=\int_{-\infty}^{z-x}(\partial F(x,y))=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty) I=\int_{u(-\infty}^{z-x}(\partial F).(\partial y/\partial u)=\int_{-\infty}^{z-x}(\partial F(x,y))=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty)](/latexrender/pictures/1232d771317899eb18bcc77fe9adf72b.png)
,q.recai na situaçao anterior...para q.
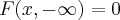
,F tem q. ser uma funçao tipo
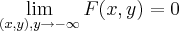
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13188 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- Função de duas variáveis
por lilianers » Qua Ago 21, 2013 19:37
- 1 Respostas
- 2361 Exibições
- Última mensagem por Renato_RJ

Qui Ago 22, 2013 12:46
Funções
-
- [Dúvida]Gráficos de funções com duas variáveis.
 por Santa Lucci » Dom Mar 13, 2011 16:58
por Santa Lucci » Dom Mar 13, 2011 16:58
- 2 Respostas
- 2318 Exibições
- Última mensagem por Santa Lucci

Dom Mar 13, 2011 21:55
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade função de duas variáveis
por ormatos » Sáb Abr 07, 2018 17:47
- 0 Respostas
- 4648 Exibições
- Última mensagem por ormatos

Sáb Abr 07, 2018 17:47
Cálculo: Limites, Derivadas e Integrais
-
- Função com mais de duas varíaveis
por LucieneHolanda » Dom Jun 03, 2012 19:18
- 4 Respostas
- 5535 Exibições
- Última mensagem por LucieneHolanda

Ter Jun 05, 2012 15:30
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx \int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx](/latexrender/pictures/eaeeab1ab797ff823bcd4fccb45baf44.png)

![\int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx \int_{-\infty}^{\infty}\left[\frac{d}{dz}\int_{-\infty}^{z-x}f_{XY}(x,y)dy\right]dx=\int_{-\infty}^{\infty}f_{XY}(x,z-x)dx](/latexrender/pictures/eaeeab1ab797ff823bcd4fccb45baf44.png)

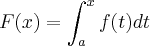 . Então F é derivável e F'(x) = f(x).
. Então F é derivável e F'(x) = f(x).
 ,pois podemos fazer como se segue:
,pois podemos fazer como se segue: ,regra de leibinitz...
,regra de leibinitz...![I=\int_{-\infty}^{z-x}\partial F(x,y)=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty) I=\int_{-\infty}^{z-x}\partial F(x,y)=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty)](/latexrender/pictures/96ce2e4b496bf5c88bc5bc1d418fd5db.png) ,sem uma definiçao de F(x,y) nada podemos concluir com
,sem uma definiçao de F(x,y) nada podemos concluir com 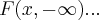

![x\in\left[a, \right b] x\in\left[a, \right b]](/latexrender/pictures/18ec34837b9a94e30aab70ad4a837bda.png) , então
, então 

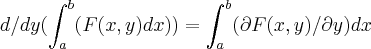 ,desde de q. F(x,y)seja continua e diferenciavel em (a,b)...qto ao exercicio e o erro...
,desde de q. F(x,y)seja continua e diferenciavel em (a,b)...qto ao exercicio e o erro...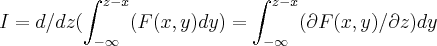 ,meu erro foi
,meu erro foi  ,mas persiste o problema do limite p/
,mas persiste o problema do limite p/

 ,
,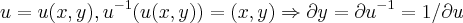

![I=\int_{u(-\infty}^{z-x}(\partial F).(\partial y/\partial u)=\int_{-\infty}^{z-x}(\partial F(x,y))=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty) I=\int_{u(-\infty}^{z-x}(\partial F).(\partial y/\partial u)=\int_{-\infty}^{z-x}(\partial F(x,y))=F(x,y)[-\infty,z-x]=F(x,z-x)-F(x,-\infty)](/latexrender/pictures/1232d771317899eb18bcc77fe9adf72b.png) ,q.recai na situaçao anterior...para q.
,q.recai na situaçao anterior...para q. 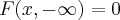 ,F tem q. ser uma funçao tipo
,F tem q. ser uma funçao tipo