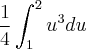por fasaatyro » Seg Dez 01, 2014 22:17
por fasaatyro » Seg Dez 01, 2014 22:17
calcule
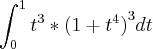
, preciso de ajuda urgente a resposta encontrada foi 15/16.
-
fasaatyro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Dez 01, 2014 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura matematica
- Andamento: cursando
 por Cleyson007 » Ter Dez 02, 2014 09:13
por Cleyson007 » Ter Dez 02, 2014 09:13
Olá, bom dia!
Sua integral pode ser resolvida tranquilamente por uma substituição simples.
Chame u = 1 + t^4
Logo, du = 3t³ dt ---> du/3 = t³dt
Não se esqueça também de alterar os limites de integração.
Quando t = 0; u = 1
Quando t = 1; u = 2
Agora é com você! Já dei as dicas
Comente qualquer dúvida

Te mandei uma mensagem privada olha lá.
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fasaatyro » Ter Dez 02, 2014 09:53
por fasaatyro » Ter Dez 02, 2014 09:53
Bom dia Cleyson agradeço a dica, mas não estou conseguindo a resposta que encontrei foi 1 e o gabarito da prova esta 15/16.
Fiz u=

du=4t³dt
1/4du =t³dt
-
fasaatyro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Dez 01, 2014 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura matematica
- Andamento: cursando
 por Cleyson007 » Ter Dez 02, 2014 12:57
por Cleyson007 » Ter Dez 02, 2014 12:57
Olá, boa tarde!
Não tem interesse na mensagem privada que lhe enviei?
ucp.php?i=pm&mode=view&f=-1&p=570O que você fez está correto. Acompanhe:
Após fazer a mudança de variável teremos de resolver essa integral que é simples
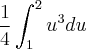

Qualquer dúvida estou a disposição

Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4348 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3684 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 3077 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2501 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3633 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
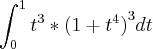 , preciso de ajuda urgente a resposta encontrada foi 15/16.
, preciso de ajuda urgente a resposta encontrada foi 15/16.

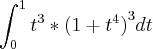 , preciso de ajuda urgente a resposta encontrada foi 15/16.
, preciso de ajuda urgente a resposta encontrada foi 15/16.