 por fasaatyro » Seg Dez 01, 2014 21:56
por fasaatyro » Seg Dez 01, 2014 21:56
![\int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx \int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx](/latexrender/pictures/a6ec631f77cc362a753bf7e7aeb23e55.png)
por favor encontrei como resultado
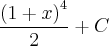
está correto????
-
fasaatyro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Dez 01, 2014 21:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura matematica
- Andamento: cursando
 por adauto martins » Ter Dez 02, 2014 16:37
por adauto martins » Ter Dez 02, 2014 16:37
seria essa I=
![\int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x}) \int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x})](/latexrender/pictures/cad4774f7b49c8fae7611b8e6646a084.png)
,se nao for,vamos nessa mesmo...
faz-se
![u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx](/latexrender/pictures/177c95970becea14daa63e93cea0fba1.png)
,logo
![I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c](/latexrender/pictures/448a13f5d8e9b626c609266dda2b22ab.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5635 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2714 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por felipealves » Ter Jun 21, 2011 11:48
- 3 Respostas
- 3992 Exibições
- Última mensagem por felipealves

Ter Jun 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] indefinida
por Aliocha Karamazov » Qui Mar 01, 2012 20:30
- 7 Respostas
- 5056 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Mar 03, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 2
por DanielFerreira » Sáb Mar 31, 2012 18:31
- 1 Respostas
- 2069 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 18:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx \int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx](/latexrender/pictures/a6ec631f77cc362a753bf7e7aeb23e55.png) por favor encontrei como resultado
por favor encontrei como resultado 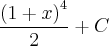 está correto????
está correto????
![\int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx \int\frac{(1+\sqrt[]{x}³}{\sqrt[]{x}}dx](/latexrender/pictures/a6ec631f77cc362a753bf7e7aeb23e55.png) por favor encontrei como resultado
por favor encontrei como resultado 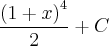 está correto????
está correto????
![\int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x}) \int_{}^{}({1+\sqrt[]{x}})^{3}dx/(\sqrt[]{x})](/latexrender/pictures/cad4774f7b49c8fae7611b8e6646a084.png) ,se nao for,vamos nessa mesmo...
,se nao for,vamos nessa mesmo...![u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx u=1+\sqrt[]{x}\Rightarrow du=(1/2).(1/\sqrt[]{x})dx](/latexrender/pictures/177c95970becea14daa63e93cea0fba1.png) ,logo
,logo ![I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c I=2.(\int_{}^{}{u}^{3}du)=2.{u}^{3+1}/(3+1)+c=(1/2)({1+\sqrt[]{x}})^{4}+c](/latexrender/pictures/448a13f5d8e9b626c609266dda2b22ab.png) ...
...


 , avisa que eu resolvo.
, avisa que eu resolvo.

