 por neoreload » Sex Nov 14, 2014 02:43
por neoreload » Sex Nov 14, 2014 02:43
Pessoal como resolve essa:
Calcular integral usando método da substituição simples por U:
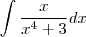
Resposta:
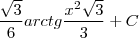
Tentei fazer e me perdi todo. Porque eu comecei fazendo assim:
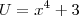
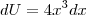
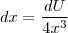
Ai substituí e ficou:
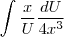
, coloquei os números para fora e cortei um X, dai ficou:

, onde achei que o du/u daria lnu, então finalmente ficou
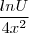
, ai coloquei o valor de U no lugar e cheguei no resultado:

, o que é bem diferente da resposta que tem na apostila. Agradeço quem puder deixar o passo a passo bem detalhado, pq estou perdido mesmo, e pelo jeito sem saber como fazer :(
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Usando método da substituição
por neoreload » Dom Nov 09, 2014 00:36
- 3 Respostas
- 3855 Exibições
- Última mensagem por e8group

Dom Nov 09, 2014 12:57
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Método da Substituição
por raimundoocjr » Sáb Jul 27, 2013 13:04
- 2 Respostas
- 2012 Exibições
- Última mensagem por raimundoocjr

Sáb Jul 27, 2013 18:02
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Indefinida] Método por Substituição
por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
- 3 Respostas
- 3009 Exibições
- Última mensagem por e8group

Dom Mar 03, 2013 18:15
Cálculo: Limites, Derivadas e Integrais
-
- Integração Usando Substituição t = tan Teta/2
por cferreira264 » Dom Jul 02, 2017 19:27
- 0 Respostas
- 1411 Exibições
- Última mensagem por cferreira264

Dom Jul 02, 2017 19:27
Cálculo: Limites, Derivadas e Integrais
-
- [Usando tecnicas de integrais por substituiçao simples]
por menino de ouro » Qua Out 24, 2012 23:10
- 1 Respostas
- 1682 Exibições
- Última mensagem por MarceloFantini

Qui Out 25, 2012 01:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
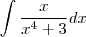
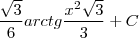
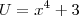
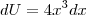
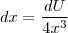
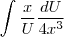 , coloquei os números para fora e cortei um X, dai ficou:
, coloquei os números para fora e cortei um X, dai ficou:  , onde achei que o du/u daria lnu, então finalmente ficou
, onde achei que o du/u daria lnu, então finalmente ficou 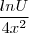 , ai coloquei o valor de U no lugar e cheguei no resultado:
, ai coloquei o valor de U no lugar e cheguei no resultado:  , o que é bem diferente da resposta que tem na apostila. Agradeço quem puder deixar o passo a passo bem detalhado, pq estou perdido mesmo, e pelo jeito sem saber como fazer :(
, o que é bem diferente da resposta que tem na apostila. Agradeço quem puder deixar o passo a passo bem detalhado, pq estou perdido mesmo, e pelo jeito sem saber como fazer :(
