 por b11adriano » Sáb Out 25, 2014 23:21
por b11adriano » Sáb Out 25, 2014 23:21
O plutônio 241 decai de acordo com a equação diferencial: dQ/dt = ? 0,00525Q. Em que Q está miligramas, e o tempo, em anos. Determine:
a) Determine a meia vida do plutônio;
b) Se 20 mg de plutônio estiverem presentes numa amostra no dia de hoje, quanto
plutônio existirá daqui a 10 anos?
c) Faça o gráfico Q = Q(t).
-
b11adriano
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Out 04, 2014 14:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: egenharia de produçao
- Andamento: cursando
 por adauto martins » Dom Out 26, 2014 15:51
por adauto martins » Dom Out 26, 2014 15:51

...
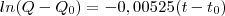
...

...
meia-vida sera:(Q/2)=(
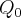
+

)/2...ai eh colocar os dados e calcular...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada de primeira ordem.
por Sobreira » Sex Mar 08, 2013 01:14
- 1 Respostas
- 1852 Exibições
- Última mensagem por Russman

Sex Mar 08, 2013 04:49
Cálculo: Limites, Derivadas e Integrais
-
- E.D.O. de primeira ordem - Aplicações
por cmantelli » Qui Mai 30, 2013 21:30
- 0 Respostas
- 877 Exibições
- Última mensagem por cmantelli

Qui Mai 30, 2013 21:30
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de primeira e segunda ordem
por Nina » Qui Nov 05, 2009 20:52
- 1 Respostas
- 4109 Exibições
- Última mensagem por marciommuniz

Sex Nov 06, 2009 13:02
Cálculo: Limites, Derivadas e Integrais
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12203 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3935 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ...
...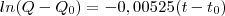 ...
... ...
...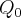 +
+ )/2...ai eh colocar os dados e calcular...
)/2...ai eh colocar os dados e calcular...

 .
.



