![\lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}} \lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}}](/latexrender/pictures/36f9bb2a2b9d469cf23a3bbe7f8fe54d.png)
Alguém pode me ajudar?
Obrigada desde já!

![\lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}} \lim_{x -> 0} \frac{f(x)- f(a)}{\sqrt[]{x} - \sqrt[]{a}}](/latexrender/pictures/36f9bb2a2b9d469cf23a3bbe7f8fe54d.png)

 e dps utilize regra operatória limites .
e dps utilize regra operatória limites .

 implica em dizer que o limite
implica em dizer que o limite 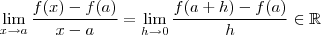 existe e uma notação para designar esta afirmação é
existe e uma notação para designar esta afirmação é  .
.  . Nosso objetivo é escrever
. Nosso objetivo é escrever 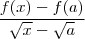 como
como  (tal que
(tal que 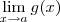 existe ) para que possamos aplicar a regra operatória do produto (vide livros de cálculo 1) .
existe ) para que possamos aplicar a regra operatória do produto (vide livros de cálculo 1) .  , nós temos que
, nós temos que 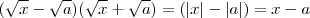 (estar implícito a positividade de
(estar implícito a positividade de  ) (*) .
) (*) . 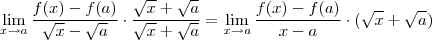 .
.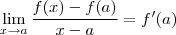 (hipótese )
(hipótese )  , então podemos aplicar a regra operatória do produto para obter
, então podemos aplicar a regra operatória do produto para obter  .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.



