 por Carolminera » Qui Jul 17, 2014 15:44
por Carolminera » Qui Jul 17, 2014 15:44
Alguém ajuda?
Estou com dificuldade para resolver o seguinte limite trigonométrico:
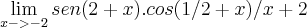
Obrigada!
-
Carolminera
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Jul 02, 2014 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Médica
- Andamento: cursando
 por DanielFerreira » Sáb Jul 19, 2014 21:09
por DanielFerreira » Sáb Jul 19, 2014 21:09
Carol, repare que a restrição do domínio é quando x é igual a zero. Uma vez que, x vale (- 2) podemos substituí-lo...
Veja:
![\\ \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right] = \\\\\\ \frac{\sin (2 - 2) \cdot \cos (\frac{1}{2} - 2)}{- 2} + 2 = \\\\\\ \frac{\sin 0 \cdot \cos (\frac{- 3}{2})}{- 2} + 2 = \\\\\\ \frac{0}{- 2} + 2 = \\\\ 0 + 2 = \\\\ \boxed{2} \\ \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right] = \\\\\\ \frac{\sin (2 - 2) \cdot \cos (\frac{1}{2} - 2)}{- 2} + 2 = \\\\\\ \frac{\sin 0 \cdot \cos (\frac{- 3}{2})}{- 2} + 2 = \\\\\\ \frac{0}{- 2} + 2 = \\\\ 0 + 2 = \\\\ \boxed{2}](/latexrender/pictures/add996da8c0b821287c83829fba3177f.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Carolminera » Dom Jul 20, 2014 12:25
por Carolminera » Dom Jul 20, 2014 12:25
Mas colocando -2 no lugar do x do denominador, não zeraria o denominador? E isso não daria uma indeterminação?
Porque o denominador é x+2, iria zerar... Estava pensando em fazer troca de variável..
-
Carolminera
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Jul 02, 2014 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Médica
- Andamento: cursando
 por DanielFerreira » Dom Jul 20, 2014 12:30
por DanielFerreira » Dom Jul 20, 2014 12:30
Ah! Equivocadamente considerei
![\lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right] \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right]](/latexrender/pictures/b4de77844d57c7f9af81791ebfff8e9c.png)
quando deveria ter feito
![\lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2 + x})}{x + 2} \right] \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2 + x})}{x + 2} \right]](/latexrender/pictures/7099502d4c2529e1993a8dc1e8991f83.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Carolminera » Dom Jul 20, 2014 21:52
por Carolminera » Dom Jul 20, 2014 21:52
Então, mas e como ficaria? A troca de variável daria certo?
-
Carolminera
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Jul 02, 2014 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Médica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] função trigonométrica
por rafaelbr91 » Ter Mar 27, 2012 17:51
- 2 Respostas
- 2171 Exibições
- Última mensagem por rafaelbr91

Ter Mar 27, 2012 18:43
Cálculo: Limites, Derivadas e Integrais
-
- Limite de uma função trigonométrica
por Douglas16 » Seg Mar 11, 2013 14:45
- 1 Respostas
- 1392 Exibições
- Última mensagem por Douglas16

Seg Mar 11, 2013 15:32
Cálculo: Limites, Derivadas e Integrais
-
- Limite de uma função trigonométrica
por Douglas16 » Sáb Mar 16, 2013 21:52
- 3 Respostas
- 2226 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 00:34
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função trigonométrica
por Fernandobertolaccini » Qua Jul 30, 2014 23:27
- 1 Respostas
- 2697 Exibições
- Última mensagem por Man Utd

Qui Ago 07, 2014 15:37
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com limite de função trigonométrica
por sofa » Qua Jun 29, 2011 04:42
- 6 Respostas
- 3622 Exibições
- Última mensagem por sofa

Qua Jun 29, 2011 06:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
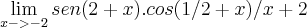

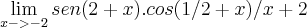

![\\ \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right] = \\\\\\ \frac{\sin (2 - 2) \cdot \cos (\frac{1}{2} - 2)}{- 2} + 2 = \\\\\\ \frac{\sin 0 \cdot \cos (\frac{- 3}{2})}{- 2} + 2 = \\\\\\ \frac{0}{- 2} + 2 = \\\\ 0 + 2 = \\\\ \boxed{2} \\ \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right] = \\\\\\ \frac{\sin (2 - 2) \cdot \cos (\frac{1}{2} - 2)}{- 2} + 2 = \\\\\\ \frac{\sin 0 \cdot \cos (\frac{- 3}{2})}{- 2} + 2 = \\\\\\ \frac{0}{- 2} + 2 = \\\\ 0 + 2 = \\\\ \boxed{2}](/latexrender/pictures/add996da8c0b821287c83829fba3177f.png)


![\lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right] \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2} + x)}{x} + 2 \right]](/latexrender/pictures/b4de77844d57c7f9af81791ebfff8e9c.png) quando deveria ter feito
quando deveria ter feito ![\lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2 + x})}{x + 2} \right] \lim_{x \rightarrow - 2} \left[ \frac{\sin (2 + x) \cdot \cos (\frac{1}{2 + x})}{x + 2} \right]](/latexrender/pictures/7099502d4c2529e1993a8dc1e8991f83.png)


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)