Se x e y são medidos em metros, a área da região entre as curvas
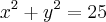e 
é 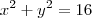igual a quanto? tento resolver, mas não da certo.
por Janoca » Sex Jun 06, 2014 17:24
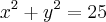e 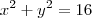é igual a quanto? tento resolver, mas não da certo.
por Janoca » Dom Jun 15, 2014 20:30
![\int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx](/latexrender/pictures/4e5fa4eab954d480f30fc54f38ad5325.png "\int_{5}^{4}\sqrt[]{25-x^2}dx + \int_{0}^{4}(\sqrt[]{25-x^2}-\sqrt[]{16-x^2})dx")
por alienante » Dom Jun 15, 2014 20:51
![[0,5]](/latexrender/pictures/be66a98c7ffb0b7cd18378674ce90c9c.png "[0,5]")
,do jeito que foi montado,esse calculo só nos mostra a área do primeiro quadrante, ignorando completamente os segundo,terceiro e quarto quadrantes.por Janoca » Dom Jun 15, 2014 21:16
por alienante » Dom Jun 15, 2014 21:42
Voltar para Cálculo: Limites, Derivadas e Integrais
por Victor Mello » Ter Nov 19, 2013 21:58
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)![{A}_{total}={A}_{maior}-{A}_{menor}=\int_{-5}^{5}\,2\,\sqrt[]{25-x^2}\,dx\,-\,\int_{-4}^{4}2\,\sqrt[]{16-x^2}\,dx=25\pi\,-\,16\pi=\,9\pi](/latexrender/pictures/e351ebb3b0a4df7903f4177b379117b9.png "{A}_{total}={A}_{maior}-{A}_{menor}=\int_{-5}^{5}\,2\,\sqrt[]{25-x^2}\,dx\,-\,\int_{-4}^{4}2\,\sqrt[]{16-x^2}\,dx=25\pi\,-\,16\pi=\,9\pi")