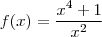 .
.O primeiro passo é encontrar a derivada primeira,
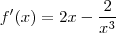 . Então eu igualo a derivada primeira a zero para encontrar as raízes.
. Então eu igualo a derivada primeira a zero para encontrar as raízes.Para resolver a equação, eu multipliquei tudo por x³ e fiquei com
 e substituí x²=y, ficando com
e substituí x²=y, ficando com 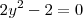 e as raízes y'=-1 e y''=1.
e as raízes y'=-1 e y''=1.Sei que agora preciso esboçar o gráfico da derivada primeira, fazer o estudo dos sinais, substituir as abscissas na função original para encontrar os pontos críticos etc, mas não sei exatamente como resolver tudo isso.
Desde já agradeço pela ajuda.



 .
.



