 por ilane » Dom Abr 27, 2014 14:06
por ilane » Dom Abr 27, 2014 14:06
\int_{0}^{1} t\sqrt{10+03t^2} d7
eu achei o seguinte resultado;
\frac{7}{9} \approx 0,777778 o o resultado seria 0 me auxiliem por favor
-
ilane
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Abr 08, 2014 10:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por e8group » Dom Abr 27, 2014 15:15
por e8group » Dom Abr 27, 2014 15:15
Zero ?? Não , não mesmo . O integrando sempre assume valores positivos quando t varia em intervalo de números não negativos ,assim a porção do gráfico da função dada pelo integrando está acima do eixo t , quando t varia em [0,1] .A menos que você digitou erroneamente a expressão .
OBS_1 .: Você está esquecendo de deixar os códigos entre as tag's tex .
O certo é
- Código: Selecionar todos
[tex] \int_0^1 t \sqrt{10 0.3t^2} [/tex]
Resultado :
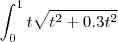
OBS_2 .: Se seu objetivo for apenas conferir o resultado você pode digitar a própria expressão em latex no wolframalpha para ver a resposta , como vemos
http://www.wolframalpha.com/input/?i=%5 ... 3t%5E2%7D+
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4613 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4581 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4345 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2844 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2869 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


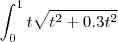


 .
.



