 por yuricastilho » Ter Abr 15, 2014 14:30
por yuricastilho » Ter Abr 15, 2014 14:30
Não consegui resolver os seguintes limites da seção 6.3 do livro de Guidorizzi.
1.a)
![\[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\]](/latexrender/pictures/eea988cefbcd315c934c93484090657e.png)
1.c)
![\[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\]](/latexrender/pictures/2f7b5ccc871e8ef61d782b9d368b8d0a.png)
1.e)
![\[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\] \[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\]](/latexrender/pictures/122c9e49ad78499eddadbd65d027ec00.png)
3.b)
![\[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\]](/latexrender/pictures/477bda5e72f2256038bde29b1f8ce445.png)
cuidado para NÃO CONFUNDIR com
![\[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\]](/latexrender/pictures/69bffcf179848289e32d255c49b2f2dc.png)
(esse eu já sei resolver)
Se alguém puder me ajudar...
-
yuricastilho
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 05, 2014 19:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por e8group » Dom Abr 27, 2014 20:03
por e8group » Dom Abr 27, 2014 20:03
Vou lhe dar uma dica mais geral que resolver todos itens (exceto o último )
Considere

qualquer número real não nulo , o limite
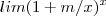
vale

(podendo
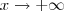
quanto a

)
De fato , deixe

e com isso
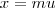
. Quando
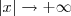
temos que

também tende a

.Das duas uma ,
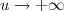
ou
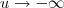
( o sinal de

que diz isso ) e assim
![lim(1+m/x)^x = lim(1+ 1/u)^{mu} = \left[ lim(1+1/u)^u \right]^m lim(1+m/x)^x = lim(1+ 1/u)^{mu} = \left[ lim(1+1/u)^u \right]^m](/latexrender/pictures/0b58087e368df4ea87d182f2ebe2aa80.png)
. Por definição
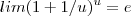
(podendo
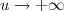
quanto a

) . Daí , o limite de expressões da forma

(

) terá sempre como resultado
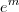
.
Agora caculemos o limite de funções racionais da forma
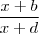
elevado a x ,
Novamente para simplificar usamos apenas lim( ...) para designar
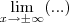
.
Segue

.
i) Defina
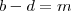
e
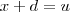
. Quando

temos que
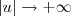
e
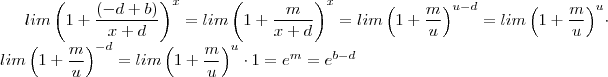
(utilizando o resultado anterior)
Obs.: Uma questão para cada tópico .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por yuricastilho » Qui Mai 01, 2014 16:28
por yuricastilho » Qui Mai 01, 2014 16:28
Muito obrigado Santhiago, ajudou imensamente.
-
yuricastilho
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 05, 2014 19:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites com número de euler]
por mpborto » Sex Mar 18, 2016 15:29
- 1 Respostas
- 2028 Exibições
- Última mensagem por adauto martins

Sex Mar 18, 2016 17:28
Cálculo: Limites, Derivadas e Integrais
-
- Limites exponenciais
por lunayanne » Dom Mar 07, 2010 00:15
- 2 Respostas
- 3352 Exibições
- Última mensagem por lucas92

Ter Abr 13, 2010 03:57
Cálculo: Limites, Derivadas e Integrais
-
- limites exponenciais
por uefs » Qua Mai 14, 2014 18:36
- 1 Respostas
- 1389 Exibições
- Última mensagem por e8group

Qui Mai 15, 2014 02:23
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES de exponenciais e logaritimos
por inkz » Qua Dez 05, 2012 16:13
- 1 Respostas
- 1686 Exibições
- Última mensagem por e8group

Qua Dez 05, 2012 20:45
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\]](/latexrender/pictures/eea988cefbcd315c934c93484090657e.png)
![\[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\]](/latexrender/pictures/2f7b5ccc871e8ef61d782b9d368b8d0a.png)
![\[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\] \[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\]](/latexrender/pictures/122c9e49ad78499eddadbd65d027ec00.png)
![\[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\]](/latexrender/pictures/477bda5e72f2256038bde29b1f8ce445.png) cuidado para NÃO CONFUNDIR com
cuidado para NÃO CONFUNDIR com ![\[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\]](/latexrender/pictures/69bffcf179848289e32d255c49b2f2dc.png) (esse eu já sei resolver)
(esse eu já sei resolver)
![\[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac2x)^x\]](/latexrender/pictures/eea988cefbcd315c934c93484090657e.png)
![\[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\] \[\lim_{x \rightarrow + \infty}(1 + \frac{1}{2x})^x\]](/latexrender/pictures/2f7b5ccc871e8ef61d782b9d368b8d0a.png)
![\[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\] \[\lim_{x \rightarrow + \infty}(\frac{x+2}{x+1})^x\]](/latexrender/pictures/122c9e49ad78499eddadbd65d027ec00.png)
![\[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{x^{2}} -1}{x})^x\]](/latexrender/pictures/477bda5e72f2256038bde29b1f8ce445.png) cuidado para NÃO CONFUNDIR com
cuidado para NÃO CONFUNDIR com ![\[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\] \[lim_{x \rightarrow 0+} (\frac{e^{2x} -1}{x})^x\]](/latexrender/pictures/69bffcf179848289e32d255c49b2f2dc.png) (esse eu já sei resolver)
(esse eu já sei resolver)
 qualquer número real não nulo , o limite
qualquer número real não nulo , o limite 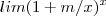 vale
vale  (podendo
(podendo 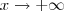 quanto a
quanto a  )
)  e com isso
e com isso 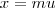 . Quando
. Quando 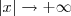 temos que
temos que  também tende a
também tende a  .Das duas uma ,
.Das duas uma , 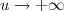 ou
ou 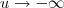 ( o sinal de
( o sinal de  que diz isso ) e assim
que diz isso ) e assim ![lim(1+m/x)^x = lim(1+ 1/u)^{mu} = \left[ lim(1+1/u)^u \right]^m lim(1+m/x)^x = lim(1+ 1/u)^{mu} = \left[ lim(1+1/u)^u \right]^m](/latexrender/pictures/0b58087e368df4ea87d182f2ebe2aa80.png) . Por definição
. Por definição 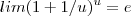 (podendo
(podendo 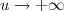 quanto a
quanto a  ) . Daí , o limite de expressões da forma
) . Daí , o limite de expressões da forma  (
(  ) terá sempre como resultado
) terá sempre como resultado 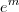 .
. 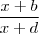 elevado a x ,
elevado a x ,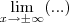 .
.  .
.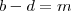 e
e 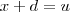 . Quando
. Quando  temos que
temos que 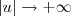 e
e 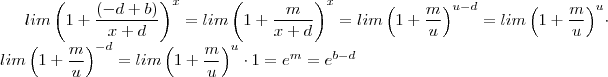 (utilizando o resultado anterior)
(utilizando o resultado anterior)
