
não preciso da resolução do exercício, só lembrar como se faz a fatoração para q eu quebre a cabeça para resolver, até por que é esse meu método de estudo.
agradeço quem poder ajudar.
Abraço!!



 e bla bla bla ... é tentar deduzir uma fórmula para
e bla bla bla ... é tentar deduzir uma fórmula para  com n = 2,3,4,5,... .
com n = 2,3,4,5,... . 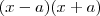 , esta fatoração já é conhecida ,entretanto para fins didáticos , dividindo a expressão
, esta fatoração já é conhecida ,entretanto para fins didáticos , dividindo a expressão  por
por  , obteremos o resultado .Qual o método utilizar ?? Um método seria o dá chave .
, obteremos o resultado .Qual o método utilizar ?? Um método seria o dá chave .  . Assim ,
. Assim , 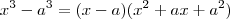
 , observamos que
, observamos que ![x^n - a^n = (x-a)(x^{n-1} + \hdots + x^2 a^{n-3} + xa^{n-2} + a^{n-1} ) = (x-a)[ x^{(n-1) -0} \cdot a^{0} + x^{(n-1 )-1} \cdot a^{1] + x^{(n-1 )-2} \cdot a^{2] + \hdots + x^{(n-1 )-(n-2)} \cdot a^{n-2} + x^{(n-1) -(n-1)} \cdot a^{n-1} x^n - a^n = (x-a)(x^{n-1} + \hdots + x^2 a^{n-3} + xa^{n-2} + a^{n-1} ) = (x-a)[ x^{(n-1) -0} \cdot a^{0} + x^{(n-1 )-1} \cdot a^{1] + x^{(n-1 )-2} \cdot a^{2] + \hdots + x^{(n-1 )-(n-2)} \cdot a^{n-2} + x^{(n-1) -(n-1)} \cdot a^{n-1}](/latexrender/pictures/cb8e3dac91da79688616b9cb643c4194.png) . A princípio , encontramos uma fórmula um pouco difícil de memorizar . Entretanto , a expressão entre colchetes , pode ser escrita sob a forma compacta
. A princípio , encontramos uma fórmula um pouco difícil de memorizar . Entretanto , a expressão entre colchetes , pode ser escrita sob a forma compacta  , e assim obtemos a fórmula
, e assim obtemos a fórmula  .
.

 e
e  é impar , teremos
é impar , teremos  .
. 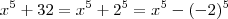 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes

 .
.
 :
: