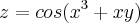 .
.Bom, no começo estava dando certo, derivei tudo em relação x, y.


Aí na hora de derivá-los na segunda ordem, o meu resultado deu:
![\frac{\partial^2 z}{\partial x^2} = -6xsen(x^3 +xy) + (-3x^2 - y)[cos(x^3+xy)(3x^2+y)] \frac{\partial^2 z}{\partial x^2} = -6xsen(x^3 +xy) + (-3x^2 - y)[cos(x^3+xy)(3x^2+y)]](/latexrender/pictures/793d6b3d84fdd92a681f135258a2e50c.png)

Só que em relação ao x, o gabarito deu
 , está bem diferente da minha pelo simples fato do termo
, está bem diferente da minha pelo simples fato do termo  aparecer uma vez só no cosseno, o meu apareceu duas vezes, será que eu errei alguma coisa, de sinal, ou algo do tipo? Eu verifiquei tudo de novo, mas deu mesma coisa. Só em relação ao y é que o gabarito correspondeu a minha resposta.
aparecer uma vez só no cosseno, o meu apareceu duas vezes, será que eu errei alguma coisa, de sinal, ou algo do tipo? Eu verifiquei tudo de novo, mas deu mesma coisa. Só em relação ao y é que o gabarito correspondeu a minha resposta.Bom, espero que tenham compreendido a minha dúvida, e obrigado!
Abraço!



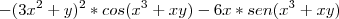 ? , assim sua resposta bateria com o gabarito.
? , assim sua resposta bateria com o gabarito.