 por magellanicLMC » Sex Fev 07, 2014 23:05
por magellanicLMC » Sex Fev 07, 2014 23:05
eu n to entendendo mt bem definição do valor médio por isso to fazendo o cálculo segundo o exemplo, se alguém pudesse me explicar o por que do que eu calculei e se ta certo agradeceria
seja
![f(x)=3\sqrt[2]{x+1} f(x)=3\sqrt[2]{x+1}](/latexrender/pictures/2625da596fd73d48764db0e128d90dbc.png)
encontre o valor médio no intervalo [-1,3]
![3\int_{-1}^{3}\sqrt[2]{x+1}dx 3\int_{-1}^{3}\sqrt[2]{x+1}dx](/latexrender/pictures/fb67a1cacaaa57a200be58e5b483a9a1.png)
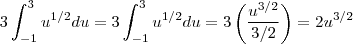
calculando dentro dos limites fica 16
como valor médio é dentro do intervalo fica

, que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?
-
magellanicLMC
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 28, 2014 20:35
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Sáb Fev 08, 2014 09:39
por e8group » Sáb Fev 08, 2014 09:39
Recomendo uma breve leitura sobre tal no link abaixo
http://www.labma.ufrj.br/~mcabral/texto ... -livro.pdf .
Indo direto à página 180 encontrará a explicação, bem como a definição .
Espero que ajude
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por magellanicLMC » Sáb Fev 08, 2014 17:00
por magellanicLMC » Sáb Fev 08, 2014 17:00
ajudou sim! obrigada, o resultado deu 4 p/ o valor médio e 7/9 para o valor de x correspondente ao valor médio, acredito que esteja certo

-
magellanicLMC
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 28, 2014 20:35
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Valor médio
 por Janoca » Ter Jun 17, 2014 01:05
por Janoca » Ter Jun 17, 2014 01:05
- 7 Respostas
- 5060 Exibições
- Última mensagem por alienante

Qua Jun 18, 2014 18:11
Cálculo: Limites, Derivadas e Integrais
-
- teorema do valor medio
por matmatco » Seg Nov 14, 2011 10:18
- 3 Respostas
- 2671 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do valor médio
por crsjcarlos » Qua Mai 01, 2013 12:09
- 1 Respostas
- 1986 Exibições
- Última mensagem por e8group

Qua Mai 01, 2013 14:07
Cálculo: Limites, Derivadas e Integrais
-
- [teorema do valor médio]
por Ge_dutra » Seg Jun 17, 2013 00:12
- 0 Respostas
- 1213 Exibições
- Última mensagem por Ge_dutra

Seg Jun 17, 2013 00:12
Cálculo: Limites, Derivadas e Integrais
-
- Duvida teorema do valor médio
por markitodq » Dom Abr 21, 2013 09:47
- 0 Respostas
- 1213 Exibições
- Última mensagem por markitodq

Dom Abr 21, 2013 09:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=3\sqrt[2]{x+1} f(x)=3\sqrt[2]{x+1}](/latexrender/pictures/2625da596fd73d48764db0e128d90dbc.png) encontre o valor médio no intervalo [-1,3]
encontre o valor médio no intervalo [-1,3]![3\int_{-1}^{3}\sqrt[2]{x+1}dx 3\int_{-1}^{3}\sqrt[2]{x+1}dx](/latexrender/pictures/fb67a1cacaaa57a200be58e5b483a9a1.png)
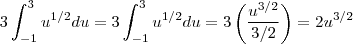
 , que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?
, que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?
![f(x)=3\sqrt[2]{x+1} f(x)=3\sqrt[2]{x+1}](/latexrender/pictures/2625da596fd73d48764db0e128d90dbc.png) encontre o valor médio no intervalo [-1,3]
encontre o valor médio no intervalo [-1,3]![3\int_{-1}^{3}\sqrt[2]{x+1}dx 3\int_{-1}^{3}\sqrt[2]{x+1}dx](/latexrender/pictures/fb67a1cacaaa57a200be58e5b483a9a1.png)
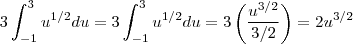
 , que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?
, que resulta em 4, alguém sabe me dizer se isso td da certo? não deveria dar um resultado dentro do intervalo?





 , avisa que eu resolvo.
, avisa que eu resolvo.

