[Calculo2: Derivada Parcial] Plano tg, Vetor Gradiente

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Calculo2: Derivada Parcial] Plano tg, Vetor Gradiente

Regras do fórum
Responder

[Calculo2: Derivada Parcial] Plano tg, Vetor Gradiente

Mensagempor Claudio Parana » Qua Fev 05, 2014 20:06

1. Considere a função f(x,y,z) = 3\frac{x+y+z}{x-y+z}

a) Calcule a taxa de variação de f em 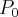{P}_{0}(1,1,1) na direção do vetor v(1,2,-2)

b) A função f aumenta ou diminui nessa direção? Justifique.

c) Qual a taxa de mais rápido decrescimento de f em 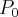{P}_{0}? E o vetor nessa direção e sentido?

d) Usando o plano tg, encontre um valor aproximado para f(0,9;1,01;0,99)


Obs: Não consigo resolvê-los e tenho dificuldades na interpretação de exercícios deste tipo (por exemplo: a expressão: "taxa de variação", letra b, "taxa de decrescimento")
Claudio Parana
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Qua Fev 05, 2014 19:26
Formação Escolar: GRADUAÇÃO
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: [Função] do primeiro grau e quadratica
Autor: Thassya - Sáb Out 01, 2011 16:20

1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?

2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?

3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?

Assunto: [Função] do primeiro grau e quadratica
Autor: Neperiano - Sáb Out 01, 2011 19:46

Ola

Qual as suas dúvidas?

O que você não está conseguindo fazer?

Nos mostre para podermos ajudar

Atenciosamente

Assunto: [Função] do primeiro grau e quadratica
Autor: joaofonseca - Sáb Out 01, 2011 20:15

1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.

y_{b}-y_{a}=m(x_{b}-x_{a})

1-3=m(-3-1) \Leftrightarrow -2=-4m \Leftrightarrow m=\frac{2}{4} \Leftrightarrow m=\frac{1}{2}

Em y=mx+b substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.

3=\frac{1}{2} \cdot 1+b\Leftrightarrow 3-\frac{1}{2}=b \Leftrightarrow b=\frac{5}{2}



2)Na equação y=x^2-5x+9 não existem zeros.Senão vejamos

Completando o quadrado,

(x^2-5x+\frac{25}{4})+9-\frac{25}{4} =0\Leftrightarrow (x-\frac{5}{2})^2+\frac{11}{4}=0

As coordenadas do vertice da parabola são (\frac{5}{2},\frac{11}{4})

O eixo de simetria é a reta x=\frac{5}{2}.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.

f(-7)=93
f(10)=59

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum