 , com b^2-4c<0
, com b^2-4c<0Obs: Isso vai chegar em uma formula de recorrencia.

 , com b^2-4c<0
, com b^2-4c<0
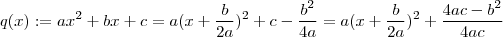 (1) . Dividimos
(1) . Dividimos  por
por  :
: 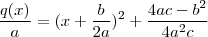 . (2)
. (2) 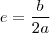 e
e 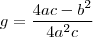 (3) . Assim ,temos
(3) . Assim ,temos  (4) e dividindo-se ambos lados por
(4) e dividindo-se ambos lados por  ,
, 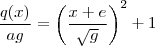 (5) ou ainda por mudança de variável
(5) ou ainda por mudança de variável  (6) ,
(6) , 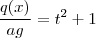 (7) . Veja o que conseguimos até agora ,
(7) . Veja o que conseguimos até agora ,  (8)
(8) 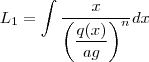 e
e  (10) .
(10) .  e escrevendo
e escrevendo  como função de
como função de  em (6) ,
em (6) ,  ,utilizando estas relações em (10), segue
,utilizando estas relações em (10), segue  . A primeira integral sabemos calcular , qual a resposta ? Já a segunda é mais trabalhosa .
. A primeira integral sabemos calcular , qual a resposta ? Já a segunda é mais trabalhosa . 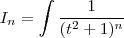 .Usando integração por partes podemos obter a fórmula(tente fazer )
.Usando integração por partes podemos obter a fórmula(tente fazer )  .
. está determinado . e
está determinado . e  pode ser determinado pela fórmula de recorrência .
pode ser determinado pela fórmula de recorrência . 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes