 por Victor Mello » Qui Nov 21, 2013 18:37
por Victor Mello » Qui Nov 21, 2013 18:37
Galera, eu estou vendo essa integral

. Ela parece ser simples, e único jeito de simplificar essa integral é multiplicar pelo fator unitário, mas infelizmente eu não estou conseguindo pensar um fator unitário que possa cair numa integral que dá para fazer pela substituição por mudança de variável logo em seguida. Eu já tentei multiplicar pelo
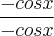
e não deu certo a substituição por mudança de variável. Mas estou pensando outras alternativas. Sei lá, pode ser que uma das identidades trigonométricas me ajude, mas a ideia não chega, infelizmente. Alguém poderia me sugerir algum fator unitário que possa simplificar essa integral, ou algum detalhe que dê certo em algumas ocasiões?
Obrigado!

-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
 por Pessoa Estranha » Qui Nov 21, 2013 20:48
por Pessoa Estranha » Qui Nov 21, 2013 20:48
Olá !
Você poderia multiplicar o numerador e o denominador pelo conjugado de (
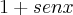
) , ou seja, por (

). Fiz um rascunho para ver se ajudava um pouco e, então, cheguei a isto:

Pode ser que ajude, mas é só uma sugestão ....
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Victor Mello » Qui Nov 21, 2013 23:27
por Victor Mello » Qui Nov 21, 2013 23:27
Ahh sim, verdade! Deu certo agora, valeu pela sugestão!

-
Victor Mello
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Nov 03, 2013 17:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da computação.
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TECNICAS DE INTEGRAÇÃO
por Marcio Cristo » Qui Dez 22, 2011 18:35
- 5 Respostas
- 3019 Exibições
- Última mensagem por LuizAquino

Sex Dez 23, 2011 18:00
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração
por Victor Mello » Seg Nov 18, 2013 23:04
- 2 Respostas
- 1639 Exibições
- Última mensagem por Victor Mello

Ter Nov 19, 2013 00:16
Cálculo: Limites, Derivadas e Integrais
-
- [tecnicas de integraçao por partes (u)(dv)]
por menino de ouro » Ter Out 30, 2012 18:21
- 3 Respostas
- 2068 Exibições
- Última mensagem por MarceloFantini

Ter Out 30, 2012 22:39
Cálculo: Limites, Derivadas e Integrais
-
- [Tecnicas de integraçao por substiuiçao simples]
por menino de ouro » Qua Out 24, 2012 16:12
- 1 Respostas
- 1495 Exibições
- Última mensagem por young_jedi

Qua Out 24, 2012 16:51
Cálculo: Limites, Derivadas e Integrais
-
- multiplicando os valores
por Ana Maria da Silva » Qua Out 23, 2013 01:04
- 1 Respostas
- 1054 Exibições
- Última mensagem por Pessoa Estranha

Qui Out 24, 2013 16:34
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Ela parece ser simples, e único jeito de simplificar essa integral é multiplicar pelo fator unitário, mas infelizmente eu não estou conseguindo pensar um fator unitário que possa cair numa integral que dá para fazer pela substituição por mudança de variável logo em seguida. Eu já tentei multiplicar pelo
. Ela parece ser simples, e único jeito de simplificar essa integral é multiplicar pelo fator unitário, mas infelizmente eu não estou conseguindo pensar um fator unitário que possa cair numa integral que dá para fazer pela substituição por mudança de variável logo em seguida. Eu já tentei multiplicar pelo 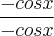 e não deu certo a substituição por mudança de variável. Mas estou pensando outras alternativas. Sei lá, pode ser que uma das identidades trigonométricas me ajude, mas a ideia não chega, infelizmente. Alguém poderia me sugerir algum fator unitário que possa simplificar essa integral, ou algum detalhe que dê certo em algumas ocasiões?
e não deu certo a substituição por mudança de variável. Mas estou pensando outras alternativas. Sei lá, pode ser que uma das identidades trigonométricas me ajude, mas a ideia não chega, infelizmente. Alguém poderia me sugerir algum fator unitário que possa simplificar essa integral, ou algum detalhe que dê certo em algumas ocasiões? 


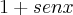 ) , ou seja, por (
) , ou seja, por ( ). Fiz um rascunho para ver se ajudava um pouco e, então, cheguei a isto:
). Fiz um rascunho para ver se ajudava um pouco e, então, cheguei a isto:







