 por Pessoa Estranha » Sex Nov 15, 2013 10:26
por Pessoa Estranha » Sex Nov 15, 2013 10:26
Olá, gostaria de ajuda na seguinte questão:
DETERMINE UMA FUNÇÃO

, DEFINIDA NUM INTERVALO ABERTO

, COM

, tal que
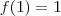
E, PARA TODO

em

,
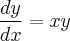
.
Resolvi da seguinte maneira:
Primeiro, precisamos observar que

. Por outro lado, temos que

. Notemos que
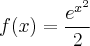
é uma possibilidade para satisfazer a proposta, contudo não satisfaz a condição de
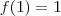
. Assim, façamos:
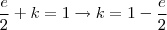
. Daí, temos:
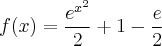
.
Tem algo errado? O resultado não é este. Tentei fazer algumas manipulações algébricas, para tentar obter o mesmo resultado, mas não consegui nada.
A resposta certa é:
![y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}} y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}}](/latexrender/pictures/73aa0904f736844495365358b40127d4.png)
.
Obrigada.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sex Nov 15, 2013 11:00
por e8group » Sex Nov 15, 2013 11:00
Muito bom exercício . Tenho uma ideia que talvez possa ajudar . Ora , se

é uma função que satisfaz a propriedade dada , então
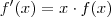
. Assumindo
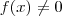
para quaisquer que seja

no intervalo aberto

,teremos que

.Agora tente integrar ambos membros com relação a variável

.
Observe que
![[ln(f(x)) ]' = ln'(f(x)) \cdot f'(x) = f'(x)/f(x) [ln(f(x)) ]' = ln'(f(x)) \cdot f'(x) = f'(x)/f(x)](/latexrender/pictures/47a05ec721da8937bc59de6527408da9.png)
(Regra da cadeia) , caso tenha dificuldade ver este resultado , faça uma substituição simples
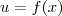
que resolve o problema .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Sex Nov 15, 2013 13:50
por Pessoa Estranha » Sex Nov 15, 2013 13:50
O que eu escrevi está errado ?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sex Nov 15, 2013 15:22
por e8group » Sex Nov 15, 2013 15:22
Pessoa Estranha escreveu:Olá, gostaria de ajuda na seguinte questão:
DETERMINE UMA FUNÇÃO

, DEFINIDA NUM INTERVALO ABERTO

, COM

, tal que
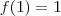
E, PARA TODO

em

,
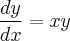
.
Resolvi da seguinte maneira:
Primeiro, precisamos observar que

. Por outro lado, temos que

. Notemos que
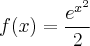
é uma possibilidade para satisfazer a proposta, contudo não satisfaz a condição de
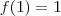
. Assim, façamos:
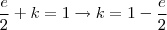
. Daí, temos:
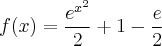
.
Tem algo errado? O resultado não é este. Tentei fazer algumas manipulações algébricas, para tentar obter o mesmo resultado, mas não consegui nada.
A resposta certa é:
![y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}} y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}}](/latexrender/pictures/73aa0904f736844495365358b40127d4.png)
.
Obrigada.
Pessoa Estranha escreveu:O que eu escrevi está errado ?
Apesar da igualdade
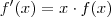
ser verdadeira quando

conforme você notou , se tomarmos

(p/ alguma constante c real ) . Temos que
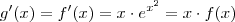
e
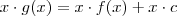
portanto , em geral ,
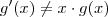
,a igualdade ocorre somente quando

já que estamos impondo que igualdade seja verdadeira para pontos arbitrários tomados no intervalo aberto

.
Observe que
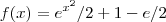
não satisfaz
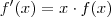
para todo x em I , apesar da mesma função satisfazer
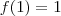
.
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Nov 15, 2013 15:43
por e8group » Sex Nov 15, 2013 15:43
Aliás , em geral a igualdade

não é verdadeira quando

, pois ,

. Entretanto,

satisfaz
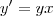
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- calculo do VAL - exercício
por nhrd » Qui Dez 11, 2008 23:40
- 0 Respostas
- 3662 Exibições
- Última mensagem por nhrd

Qui Dez 11, 2008 23:40
Matemática Financeira
-
- Cálculo em exercício
por Sofiaxavier » Ter Out 19, 2010 20:08
- 1 Respostas
- 1358 Exibições
- Última mensagem por MarceloFantini

Ter Out 19, 2010 20:32
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Exercício
por Pessoa Estranha » Sáb Dez 28, 2013 15:45
- 5 Respostas
- 2779 Exibições
- Última mensagem por Pessoa Estranha

Sex Jan 03, 2014 17:36
Cálculo: Limites, Derivadas e Integrais
-
- Exercício calculo III
 por HenriqueGS » Dom Jun 05, 2016 20:27
por HenriqueGS » Dom Jun 05, 2016 20:27
- 3 Respostas
- 3680 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 11, 2016 08:42
Cálculo: Limites, Derivadas e Integrais
-
- Exercicio Calculo 3
por leocr » Qua Set 20, 2017 11:16
- 0 Respostas
- 2052 Exibições
- Última mensagem por leocr

Qua Set 20, 2017 11:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , DEFINIDA NUM INTERVALO ABERTO
, DEFINIDA NUM INTERVALO ABERTO  , COM
, COM  , tal que
, tal que 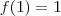 E, PARA TODO
E, PARA TODO  em
em  ,
, 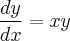 .
. . Por outro lado, temos que
. Por outro lado, temos que  . Notemos que
. Notemos que 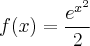 é uma possibilidade para satisfazer a proposta, contudo não satisfaz a condição de
é uma possibilidade para satisfazer a proposta, contudo não satisfaz a condição de 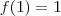 . Assim, façamos:
. Assim, façamos: 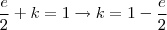 . Daí, temos:
. Daí, temos: 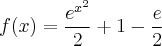 .
.![y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}} y = \frac{1}{\sqrt[]{e}} {e}^{\frac{{x}^{2}}{2}}](/latexrender/pictures/73aa0904f736844495365358b40127d4.png) .
.

 é uma função que satisfaz a propriedade dada , então
é uma função que satisfaz a propriedade dada , então 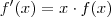 . Assumindo
. Assumindo 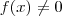 para quaisquer que seja
para quaisquer que seja  .Agora tente integrar ambos membros com relação a variável
.Agora tente integrar ambos membros com relação a variável ![[ln(f(x)) ]' = ln'(f(x)) \cdot f'(x) = f'(x)/f(x) [ln(f(x)) ]' = ln'(f(x)) \cdot f'(x) = f'(x)/f(x)](/latexrender/pictures/47a05ec721da8937bc59de6527408da9.png) (Regra da cadeia) , caso tenha dificuldade ver este resultado , faça uma substituição simples
(Regra da cadeia) , caso tenha dificuldade ver este resultado , faça uma substituição simples 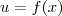 que resolve o problema .
que resolve o problema . conforme você notou , se tomarmos
conforme você notou , se tomarmos  (p/ alguma constante c real ) . Temos que
(p/ alguma constante c real ) . Temos que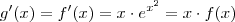 e
e 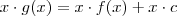
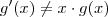 ,a igualdade ocorre somente quando
,a igualdade ocorre somente quando  já que estamos impondo que igualdade seja verdadeira para pontos arbitrários tomados no intervalo aberto
já que estamos impondo que igualdade seja verdadeira para pontos arbitrários tomados no intervalo aberto 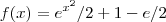 não satisfaz
não satisfaz 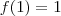 .
. não é verdadeira quando
não é verdadeira quando  , pois ,
, pois ,  . Entretanto,
. Entretanto, satisfaz
satisfaz 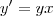 .
.



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.