


 são dadas implicitamente por
são dadas implicitamente por 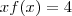 e
e  (aqui trocamos y por g,f ).
(aqui trocamos y por g,f ). se intersectam apenas na origem (é fácil ver! ) . Agora suponhamos que o par ordenado (a,b) pertence ao gráfico das funções
se intersectam apenas na origem (é fácil ver! ) . Agora suponhamos que o par ordenado (a,b) pertence ao gráfico das funções  .Então :
.Então :  ,logo
,logo 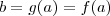 . Ou seja ,
. Ou seja , 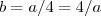 . Resolvendo , encontrará
. Resolvendo , encontrará 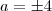 .
. 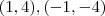 .
. 

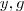 para
para ![x \in [0,1] x \in [0,1]](/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) e a segunda limitada pelas funções
e a segunda limitada pelas funções  para
para ![x \in [1,4] x \in [1,4]](/latexrender/pictures/11ae500ff75c5975ea2c6c84d52db548.png) . As áreas destas regiões podem ser obtidas respc. por :
. As áreas destas regiões podem ser obtidas respc. por : 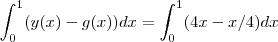
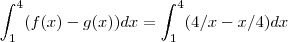 .
. 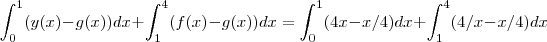 ou ainda se preferir :
ou ainda se preferir : 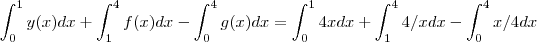 .
. 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)