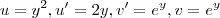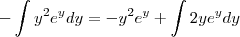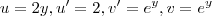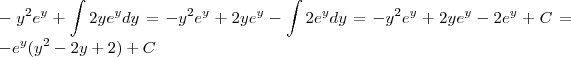por marinalcd » Qua Set 18, 2013 15:45
por marinalcd » Qua Set 18, 2013 15:45
Tenho que resolver a seguinte integral pelo método de integração por partes:
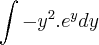
Fiz assim:
u=y² ; du = 2y dy.
dv =
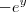
; v =
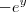
.
Então a integral ficaria:
-y²
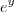
-
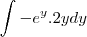
resolvendo essa outra integral também por partes, cheguei em : 2y
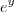
-
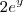
+c.
Mas no gabarito está que a solução dessa última integral é 2y
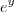
-
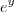
+c.
Não consegui entender o porquê do 2 não estar multiplicando o exponencial. Alguém sabe me dizer?
Obrigada!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por temujin » Sex Set 20, 2013 21:12
por temujin » Sex Set 20, 2013 21:12
Olá.
Não tá faltando algo aí??
Veja:
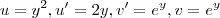
Logo,
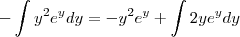
De novo por partes:
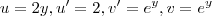
Logo,
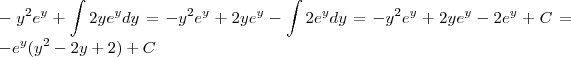
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4584 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qua Jun 01, 2011 22:05
- 2 Respostas
- 2313 Exibições
- Última mensagem por rita becher

Qui Jun 02, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qui Jun 02, 2011 00:20
- 4 Respostas
- 4003 Exibições
- Última mensagem por rita becher

Sáb Jun 04, 2011 13:01
Cálculo: Limites, Derivadas e Integrais
-
- Integral por Partes
por Guilherme Carvalho » Ter Mar 06, 2012 23:08
- 2 Respostas
- 2106 Exibições
- Última mensagem por Guilherme Carvalho

Qua Mar 07, 2012 10:39
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por gasparina nunes » Sáb Abr 07, 2012 23:42
- 3 Respostas
- 2558 Exibições
- Última mensagem por fraol

Dom Abr 08, 2012 22:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
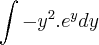
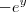 ; v =
; v = 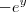 .
.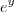 -
- 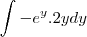
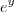 -
- 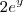 +c.
+c.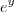 -
- 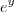 +c.
+c.