 por Ana Maria da Silva » Sáb Set 14, 2013 17:13
por Ana Maria da Silva » Sáb Set 14, 2013 17:13
Derevando y em relação a x,

, onde y é dado implicitamente pela equação,

temos
a-

=
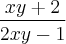
b-

c-

d-
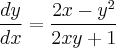
e-

Preciso ver o desenvolvimento agradeço!
-
Ana Maria da Silva
- Usuário Parceiro

-
- Mensagens: 83
- Registrado em: Qua Mar 27, 2013 15:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , onde y é dado implicitamente pela equação,
, onde y é dado implicitamente pela equação, temos
temos =
=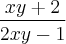


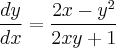


 , onde y é dado implicitamente pela equação,
, onde y é dado implicitamente pela equação, temos
temos =
=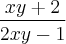


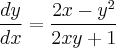



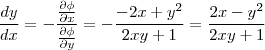


 .
.
 :
: