 por Matheus Lacombe O » Dom Ago 04, 2013 18:26
por Matheus Lacombe O » Dom Ago 04, 2013 18:26
Olá! tentei resolver a questão 6.3.70 (HOWARD Anton, Calculo- 8º edição, p.373) mas minhas respostas sempre dão fracionárias (como pode 0,37 rã??) e eu não consegui o gabarito desta questão que é par.
- A seguinte questão diz que um certo lago possui uma quantidade de rãs em um ano e quer saber a quantidade de rãs em 't' anos depois, com base em um modelo matemático de crescimento, sendo que o livro só da a derivada desse modelo de crescimento.
Enunciado na integra:
http://uploaddeimagens.com.br/imagens/enunciado-png![\frac{d}{dt}\left[p(t)\right]={(3+0,12t)}^{\frac{3}{2}} \frac{d}{dt}\left[p(t)\right]={(3+0,12t)}^{\frac{3}{2}}](/latexrender/pictures/3b7fa3598000d8247a11bc9e128b8c74.png)
![\int_{}^{}\frac{d}{dt}\left[p(t)\right]dt=\int_{}^{}{(3+0,12t)}^{\frac{3}{2}}dt \int_{}^{}\frac{d}{dt}\left[p(t)\right]dt=\int_{}^{}{(3+0,12t)}^{\frac{3}{2}}dt](/latexrender/pictures/a460f856816381e47d69cb0f970e7d02.png)
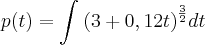


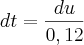
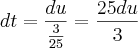

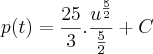

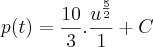
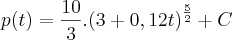
de 2005 a 2010 - 5 anos. t=5
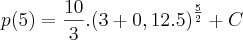
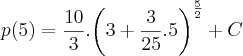
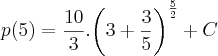

![p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{5}}+C p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{5}}+C](/latexrender/pictures/61faa0f5c1ce0c29bf01e6d5a0aff176.png)
![p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{2}.{\left(\frac{18}{5}\right)}^{2}.\left(\frac{18}{5}\right)}+C p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{2}.{\left(\frac{18}{5}\right)}^{2}.\left(\frac{18}{5}\right)}+C](/latexrender/pictures/4377d0f73553cc50829a299524c69fbc.png)
![p(5)=\frac{10}{3}.\frac{18}{5}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C p(5)=\frac{10}{3}.\frac{18}{5}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C](/latexrender/pictures/e57163560a55b4752b1fd48b642143fa.png)
![p(5)=\frac{2}{1}.\frac{6}{1}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C p(5)=\frac{2}{1}.\frac{6}{1}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C](/latexrender/pictures/bb4bd9d0bbd359809010c23ae87b8ab7.png)
![p(5)=\frac{216}{5}.\frac{\sqrt[]{18}}{\sqrt[]{5}}+C p(5)=\frac{216}{5}.\frac{\sqrt[]{18}}{\sqrt[]{5}}+C](/latexrender/pictures/4d177941549ce8d7ecaa3c9b96c43834.png)
![p(5)=\frac{216}{5}.\frac{3\sqrt[]{2}}{\sqrt[]{5}}+C p(5)=\frac{216}{5}.\frac{3\sqrt[]{2}}{\sqrt[]{5}}+C](/latexrender/pictures/838ce66453f4188933b8c3b92c4c5741.png)
![p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+C p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+C](/latexrender/pictures/a3c44b93865cb1179525f8a250c33abc.png)
- Bom.. Sabendo que no ponto '0', ou seja, no ano '0', que é o ano de 2005, há 100.000 rãs..


![100000=\frac{10}{3}.\sqrt[]{{3}^{5}}+C 100000=\frac{10}{3}.\sqrt[]{{3}^{5}}+C](/latexrender/pictures/7fa7d3a7e9b052a8861b9a0731823fb3.png)
![100000=\frac{10}{3}.\sqrt[]{{3}^{2}.{3}^{2}.3}+C 100000=\frac{10}{3}.\sqrt[]{{3}^{2}.{3}^{2}.3}+C](/latexrender/pictures/9aa7e5a036ad06198be361f09fab78db.png)
![100000=\frac{10}{3}.3.3\sqrt[]{3}+C 100000=\frac{10}{3}.3.3\sqrt[]{3}+C](/latexrender/pictures/3fd367d1b5eb4f993ba8c7860c1d0288.png)
![100000=10.3\sqrt[]{3}+C 100000=10.3\sqrt[]{3}+C](/latexrender/pictures/a2475a9c33ebed0739a2e9daa15c34ac.png)
![100000=30\sqrt[]{3}+C 100000=30\sqrt[]{3}+C](/latexrender/pictures/a485e6e8774d7c0472e4409bc156eb77.png)
![C=100000-30\sqrt[]{3} C=100000-30\sqrt[]{3}](/latexrender/pictures/6cd7f3e1a2c670fdc079dfc687523d68.png)
- logo:
![p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+100000-30\sqrt[]{3} p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+100000-30\sqrt[]{3}](/latexrender/pictures/a901d7995f1a5fe0ea33a0796ab3358c.png)
- E agora???? Essa não pode ser a resposta, pode?
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por Russman » Seg Ago 05, 2013 11:03
por Russman » Seg Ago 05, 2013 11:03
Pode sim, pq não?
Calcule uma aproximação inteira do valor qe você calculou.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Matheus Lacombe O » Ter Ago 06, 2013 13:56
por Matheus Lacombe O » Ter Ago 06, 2013 13:56
Ummmm... Mas, então ta certo??
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por Russman » Ter Ago 06, 2013 13:59
por Russman » Ter Ago 06, 2013 13:59
Acredito que sim.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral Indefinida] Aplicada à projeções de população
por Matheus Lacombe O » Qui Mar 14, 2013 12:57
- 1 Respostas
- 1921 Exibições
- Última mensagem por Russman

Qui Mar 14, 2013 14:08
Cálculo: Limites, Derivadas e Integrais
-
- Tamanho da amostra - população heterogenia e pequena
por Roniberto » Sex Fev 13, 2009 15:41
- 2 Respostas
- 2871 Exibições
- Última mensagem por Roniberto

Ter Fev 17, 2009 09:22
Estatística
-
- Que teste usar numa população não normal
por citadp » Ter Jan 21, 2014 08:20
- 0 Respostas
- 971 Exibições
- Última mensagem por citadp

Ter Jan 21, 2014 08:20
Estatística
-
- Como descobrir o restante gasto pela população
por rsene » Qui Mai 26, 2011 09:33
- 0 Respostas
- 791 Exibições
- Última mensagem por rsene

Qui Mai 26, 2011 09:33
Estatística
-
- Crescimento Exponencial
por brunotst » Dom Set 05, 2010 10:18
- 3 Respostas
- 4266 Exibições
- Última mensagem por Douglasm

Dom Set 05, 2010 13:20
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{d}{dt}\left[p(t)\right]={(3+0,12t)}^{\frac{3}{2}} \frac{d}{dt}\left[p(t)\right]={(3+0,12t)}^{\frac{3}{2}}](/latexrender/pictures/3b7fa3598000d8247a11bc9e128b8c74.png)
![\int_{}^{}\frac{d}{dt}\left[p(t)\right]dt=\int_{}^{}{(3+0,12t)}^{\frac{3}{2}}dt \int_{}^{}\frac{d}{dt}\left[p(t)\right]dt=\int_{}^{}{(3+0,12t)}^{\frac{3}{2}}dt](/latexrender/pictures/a460f856816381e47d69cb0f970e7d02.png)
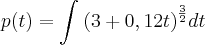


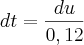
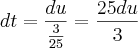

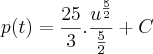

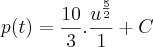
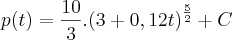
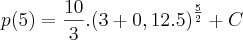
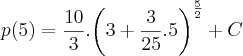
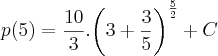

![p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{5}}+C p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{5}}+C](/latexrender/pictures/61faa0f5c1ce0c29bf01e6d5a0aff176.png)
![p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{2}.{\left(\frac{18}{5}\right)}^{2}.\left(\frac{18}{5}\right)}+C p(5)=\frac{10}{3}.\sqrt[]{{\left(\frac{18}{5}\right)}^{2}.{\left(\frac{18}{5}\right)}^{2}.\left(\frac{18}{5}\right)}+C](/latexrender/pictures/4377d0f73553cc50829a299524c69fbc.png)
![p(5)=\frac{10}{3}.\frac{18}{5}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C p(5)=\frac{10}{3}.\frac{18}{5}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C](/latexrender/pictures/e57163560a55b4752b1fd48b642143fa.png)
![p(5)=\frac{2}{1}.\frac{6}{1}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C p(5)=\frac{2}{1}.\frac{6}{1}.\frac{18}{5}\sqrt[]{\frac{18}{5}}+C](/latexrender/pictures/bb4bd9d0bbd359809010c23ae87b8ab7.png)
![p(5)=\frac{216}{5}.\frac{\sqrt[]{18}}{\sqrt[]{5}}+C p(5)=\frac{216}{5}.\frac{\sqrt[]{18}}{\sqrt[]{5}}+C](/latexrender/pictures/4d177941549ce8d7ecaa3c9b96c43834.png)
![p(5)=\frac{216}{5}.\frac{3\sqrt[]{2}}{\sqrt[]{5}}+C p(5)=\frac{216}{5}.\frac{3\sqrt[]{2}}{\sqrt[]{5}}+C](/latexrender/pictures/838ce66453f4188933b8c3b92c4c5741.png)
![p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+C p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+C](/latexrender/pictures/a3c44b93865cb1179525f8a250c33abc.png)


![100000=\frac{10}{3}.\sqrt[]{{3}^{5}}+C 100000=\frac{10}{3}.\sqrt[]{{3}^{5}}+C](/latexrender/pictures/7fa7d3a7e9b052a8861b9a0731823fb3.png)
![100000=\frac{10}{3}.\sqrt[]{{3}^{2}.{3}^{2}.3}+C 100000=\frac{10}{3}.\sqrt[]{{3}^{2}.{3}^{2}.3}+C](/latexrender/pictures/9aa7e5a036ad06198be361f09fab78db.png)
![100000=\frac{10}{3}.3.3\sqrt[]{3}+C 100000=\frac{10}{3}.3.3\sqrt[]{3}+C](/latexrender/pictures/3fd367d1b5eb4f993ba8c7860c1d0288.png)
![100000=10.3\sqrt[]{3}+C 100000=10.3\sqrt[]{3}+C](/latexrender/pictures/a2475a9c33ebed0739a2e9daa15c34ac.png)
![100000=30\sqrt[]{3}+C 100000=30\sqrt[]{3}+C](/latexrender/pictures/a485e6e8774d7c0472e4409bc156eb77.png)
![C=100000-30\sqrt[]{3} C=100000-30\sqrt[]{3}](/latexrender/pictures/6cd7f3e1a2c670fdc079dfc687523d68.png)
![p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+100000-30\sqrt[]{3} p(5)=\frac{648\sqrt[]{2}}{5\sqrt[]{5}}+100000-30\sqrt[]{3}](/latexrender/pictures/a901d7995f1a5fe0ea33a0796ab3358c.png)



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.