Questões: 25 e 26
http://www.dma.ufv.br/downloads/MAT%201 ... 012-II.pdf
Vlw, pela ajuda!



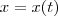 e
e  os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por
os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por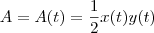
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)]](/latexrender/pictures/1a34075169e113ffc583d801742964d0.png)
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ]](/latexrender/pictures/cdeb48e51d261a2ada33e8fa596743a2.png)
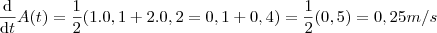 .
.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.