 por armando » Ter Jul 23, 2013 19:38
por armando » Ter Jul 23, 2013 19:38
Olá pessoal.
Como resolver o seguinte Integral:
O que faço com aquele
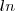
?
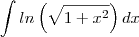
Grato
armando
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Ter Jul 23, 2013 22:01
por MateusL » Ter Jul 23, 2013 22:01
Armando,
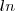
é o logarítmo natural.
Procurando em uma tábua de integrais:
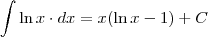
Mas terás que fazer uma substituição para resolver a integral que escrevestes.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por armando » Dom Jul 28, 2013 21:46
por armando » Dom Jul 28, 2013 21:46
Oi MateusL
Pode me explicar como fica essa substituição ? É que estou aprendendo esta matéria, e esse negócio da substituição ainda é muito confuso pra mim.
Coloquei a questão no WolframAlpha, no dispositivo de resolução step by step, e me deu como solução:
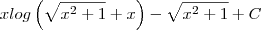
Não deveria ser
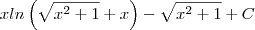
Nota__ Contudo, no fim, após a solução diz :
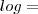 Logaritmo natural»
Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
Grato:
armando
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Dom Jul 28, 2013 23:31
por MateusL » Dom Jul 28, 2013 23:31
Olá Armando.
O

no Wolfram é a mesma coisa que o

. Notações diferentes para a mesma coisa.
A integral que encontrastes é a integral da função
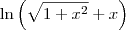
, mas no enunciado escrevestes
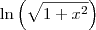
.
Agora fiquei na dúvida de qual função você quer descobrir a integral:
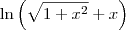
ou
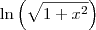
?
Ah, acho que me enganei quando disse que deverias resolver por substituição.
Acredito que terás que resolver por partes.
Abraço
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por armando » Seg Jul 29, 2013 11:15
por armando » Seg Jul 29, 2013 11:15
Oi MateusL
Desculpe, de facto, o enunciado correto é o da ultima versão.
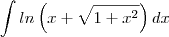
Obrigado pelo reparo.
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Seg Jul 29, 2013 14:48
por MateusL » Seg Jul 29, 2013 14:48
Então vamos à resolução:
Pela integração por partes, sabemos que:
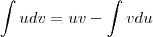
Façamos:
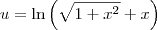

Então
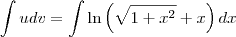
Teremos, fazendo
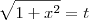
para facilitar a notação:
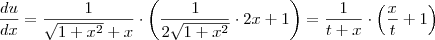
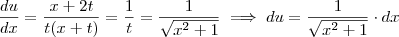
E também:
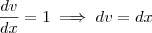
Assim:
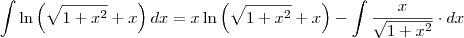
Notemos que:
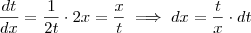
Então:
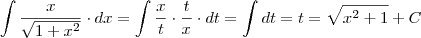
Portanto:
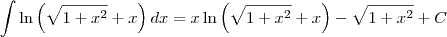
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
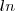 ?
?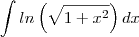

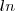 ?
?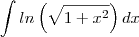

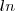 é o logarítmo natural.
é o logarítmo natural.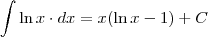

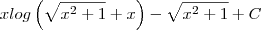
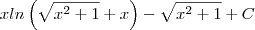
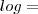 Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
Logaritmo natural». Sendo as aspas um linke para outra página com explicação detalhada sobre o assunto.
 no Wolfram é a mesma coisa que o
no Wolfram é a mesma coisa que o  . Notações diferentes para a mesma coisa.
. Notações diferentes para a mesma coisa.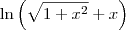 , mas no enunciado escrevestes
, mas no enunciado escrevestes 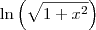 .
.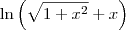 ou
ou 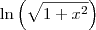 ?
?
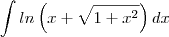

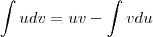
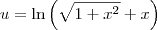

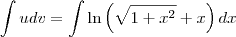
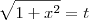 para facilitar a notação:
para facilitar a notação: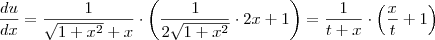
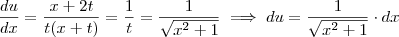
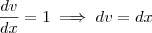
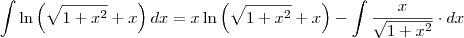
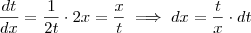
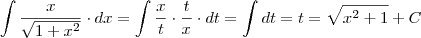
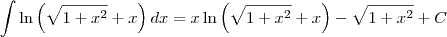

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.