 por ghiza » Seg Jul 15, 2013 11:23
por ghiza » Seg Jul 15, 2013 11:23
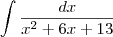
chegei em

u=x+3
logo,
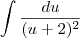
t=u+2


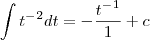
agora substituindo
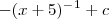
isso está correto?
Editado pela última vez por
ghiza em Seg Jul 15, 2013 13:22, em um total de 1 vez.
-
ghiza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Jul 14, 2013 21:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. alimentos
- Andamento: cursando
 por e8group » Seg Jul 15, 2013 12:36
por e8group » Seg Jul 15, 2013 12:36
Só compreendi a primeira parte que você completou quadrados (parte esta correta ) .As outras partes não compreendi devido ao erro com LaTeX . A motivação de completar quadrados e utilizar substituição simples é o fato da composição de funções . Observando o integrando já podemos dizer que a resposta da integral terá o formato

onde g é uma função que vamos determinar ( Nota :

) .
Usando que
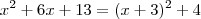
e deixando

em evidência ,segue :

.
Agora a substituição simples
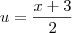
resolve o problema .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por ghiza » Seg Jul 15, 2013 13:24
por ghiza » Seg Jul 15, 2013 13:24
corrigi os erros nas formulas. mas acho que é como foi fez mesmo. valeu
-
ghiza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Jul 14, 2013 21:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. alimentos
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como calcular essa integral ?!
por lucasAS » Dom Jun 01, 2014 16:44
- 1 Respostas
- 1563 Exibições
- Última mensagem por e8group

Qua Jun 04, 2014 16:00
Cálculo: Limites, Derivadas e Integrais
-
- Como calcular a integral indefinida por substituição
 por Therodrigou » Dom Ago 26, 2018 23:13
por Therodrigou » Dom Ago 26, 2018 23:13
- 2 Respostas
- 6313 Exibições
- Última mensagem por Therodrigou

Ter Ago 28, 2018 00:23
Cálculo: Limites, Derivadas e Integrais
-
- Como calcular este integral? Duvida basica
por JorgeMartel » Ter Jul 19, 2011 11:48
- 1 Respostas
- 1729 Exibições
- Última mensagem por Molina

Ter Jul 19, 2011 12:35
Cálculo: Limites, Derivadas e Integrais
-
- como calcular 3 = (1+5i)(1+i)^8
por elpidiomelo » Seg Nov 16, 2009 18:38
- 5 Respostas
- 3816 Exibições
- Última mensagem por thadeu

Qua Nov 18, 2009 12:26
Funções
-
- como calcular x - x^1/2 + 4 = 2
por jdf01 » Ter Mai 10, 2011 15:52
- 2 Respostas
- 2985 Exibições
- Última mensagem por jdf01

Qua Mai 11, 2011 21:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
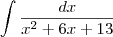

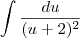


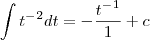
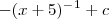

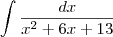

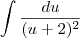


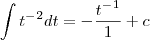
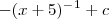

 onde g é uma função que vamos determinar ( Nota :
onde g é uma função que vamos determinar ( Nota :  ) .
) . 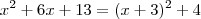 e deixando
e deixando  em evidência ,segue :
em evidência ,segue :  .
. 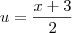 resolve o problema .
resolve o problema .



 , avisa que eu resolvo.
, avisa que eu resolvo.

