 por _bruno94 » Qui Jun 06, 2013 13:39
por _bruno94 » Qui Jun 06, 2013 13:39
Pessoal, me ajudem com este limite por favor:
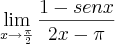
Obrigado! : )
-
_bruno94
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 07, 2013 22:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por e8group » Qui Jun 06, 2013 21:17
por e8group » Qui Jun 06, 2013 21:17
Dicas :
(i) Deixe o número 2 em evidência no denominador ,obtendo

.
(ii) Reescreva
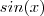
como
![sin(x + 0) = sin(x +[\pi/2 - \pi/2]) = sin([x-\pi/2] + \pi/2) =sin(x-\pi/2)cos(\pi/2) + sin(\pi/2) cos(x-\pi/2) = cos(x-\pi/2) sin(x + 0) = sin(x +[\pi/2 - \pi/2]) = sin([x-\pi/2] + \pi/2) =sin(x-\pi/2)cos(\pi/2) + sin(\pi/2) cos(x-\pi/2) = cos(x-\pi/2)](/latexrender/pictures/216920800e41e7dbac99d5273fc8bd31.png)
(iii) Faça mudança de variável ,

e observe que para

tem-se
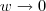
.
(iv) Multiplique o numerador e denominador por

e utilize que

.
Agora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por _bruno94 » Sáb Jun 08, 2013 19:31
por _bruno94 » Sáb Jun 08, 2013 19:31
Valeu, cara. Consegui resolver direitinho. Obrigado.

-
_bruno94
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 07, 2013 22:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7256 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] calculo de limite trigonométrico
por PRADO » Dom Mai 22, 2016 17:01
- 2 Respostas
- 5615 Exibições
- Última mensagem por PRADO

Sex Jun 03, 2016 23:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonometrico
por Ge_dutra » Qua Jan 30, 2013 23:38
- 2 Respostas
- 2046 Exibições
- Última mensagem por Ge_dutra

Qui Jan 31, 2013 22:30
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite Trigonométrico
 por viniciushenrique1995 » Ter Out 28, 2014 00:20
por viniciushenrique1995 » Ter Out 28, 2014 00:20
- 1 Respostas
- 1872 Exibições
- Última mensagem por adauto martins

Ter Out 28, 2014 17:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
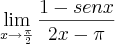

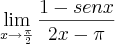

 .
. 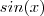 como
como ![sin(x + 0) = sin(x +[\pi/2 - \pi/2]) = sin([x-\pi/2] + \pi/2) =sin(x-\pi/2)cos(\pi/2) + sin(\pi/2) cos(x-\pi/2) = cos(x-\pi/2) sin(x + 0) = sin(x +[\pi/2 - \pi/2]) = sin([x-\pi/2] + \pi/2) =sin(x-\pi/2)cos(\pi/2) + sin(\pi/2) cos(x-\pi/2) = cos(x-\pi/2)](/latexrender/pictures/216920800e41e7dbac99d5273fc8bd31.png)
 e observe que para
e observe que para  tem-se
tem-se 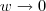 .
. e utilize que
e utilize que  .
. 



 .
.
 :
: