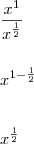por Thyago Quimica » Qua Mai 29, 2013 15:47
por Thyago Quimica » Qua Mai 29, 2013 15:47
Pelo posicionamento no livro ela teve ser bem simples, mais não to conseguindo fazer. Resp.: 20/3
![\int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx \int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx](/latexrender/pictures/796281c52df68bc6cc5c9fd2a904937a.png)
-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Lennon » Sáb Jun 08, 2013 03:01
por Lennon » Sáb Jun 08, 2013 03:01
-
Lennon
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Mai 12, 2013 17:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Thyago Quimica » Sáb Jun 08, 2013 17:01
por Thyago Quimica » Sáb Jun 08, 2013 17:01
Obrigado pela ajuda Lennon
cheguei ao resultado, só não entendi como o
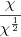
virou
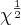
que propriedade é essa ?
-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Man Utd » Sáb Jun 08, 2013 18:08
por Man Utd » Sáb Jun 08, 2013 18:08
Thyago Quimica escreveu:Obrigado pela ajuda Lennon
cheguei ao resultado, só não entendi como o
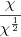
virou
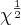
que propriedade é essa ?
olá.
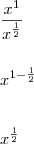
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL] Soma de Riemann
por Aryane » Dom Jan 06, 2013 12:10
- 0 Respostas
- 1308 Exibições
- Última mensagem por Aryane

Dom Jan 06, 2013 12:10
Cálculo: Limites, Derivadas e Integrais
-
- [Integral]Soma de Riemann
por armando » Seg Ago 12, 2013 23:43
- 1 Respostas
- 1528 Exibições
- Última mensagem por Russman

Ter Ago 13, 2013 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral]Soma de Riemann
por armando » Seg Ago 12, 2013 23:48
- 0 Respostas
- 1078 Exibições
- Última mensagem por armando

Seg Ago 12, 2013 23:48
Cálculo: Limites, Derivadas e Integrais
-
- Integral e Soma Dupla de Riemann - Por Favor, Urgente!
por Bruhh » Seg Mai 09, 2011 20:17
- 5 Respostas
- 3507 Exibições
- Última mensagem por Bruhh

Ter Mai 10, 2011 19:33
Cálculo: Limites, Derivadas e Integrais
-
- Somas de Riemann
por andrerodrigues98 » Ter Dez 01, 2015 21:14
- 0 Respostas
- 1249 Exibições
- Última mensagem por andrerodrigues98

Ter Dez 01, 2015 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx \int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx](/latexrender/pictures/796281c52df68bc6cc5c9fd2a904937a.png)


![\int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx \int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx](/latexrender/pictures/796281c52df68bc6cc5c9fd2a904937a.png)

![\int_{1}^{4}\frac{1}{\sqrt[]{x}}+\frac{x}{\sqrt[]{x}} \int_{1}^{4}\frac{1}{\sqrt[]{x}}+\frac{x}{\sqrt[]{x}}](/latexrender/pictures/d69886d9863983f3f86b0bfd30c586ad.png)
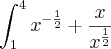
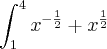

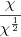 virou
virou 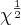 que propriedade é essa ?
que propriedade é essa ?
virou
que propriedade é essa ?