 por ericaguedes_ » Sex Jun 07, 2013 23:58
por ericaguedes_ » Sex Jun 07, 2013 23:58
Alguém poderia me ajudar, por favor? Meu resultado tem dado a=b=1/2, mas está errado. :(

Obrigada desde já!!
-
ericaguedes_
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Mai 19, 2013 11:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Sáb Jun 08, 2013 12:40
por e8group » Sáb Jun 08, 2013 12:40
(i)
Só para fixar as ideias ,imagine que tenhamos um
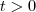
suficiente pequeno de modo que a diferença

e o acréscimo de

em

se aproxima cada vez mais de

.Suponha que a função
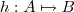
esteja definida em

e
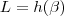
.Se

parece razoável dizer que para quaisquer números

em

sempre
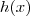
se aproxima de

já que

,mas isto não necessariamente acontece ,é o caso das funções descontínuas em

.
(ii) Suponha

.Vamos aplicar o raciocínio (i) em seu exercício .Como
![D_f =[-3,3] D_f =[-3,3]](/latexrender/pictures/94c49f5ccf37caed6252934a0b3cb415.png)
basta impor que quando
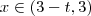
,tem-se sempre

,ou seja ,
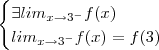
.Desta forma você obterá

que satisfaça a continuidade da função no ponto 3 .Analogamente ,você achará

que satisfaça a continuidade de

no ponto -3 ,basta impor

.
Tente concluir e comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite- Continuidade em intervalos
por killerkill » Sáb Ago 13, 2011 02:25
- 7 Respostas
- 7926 Exibições
- Última mensagem por killerkill

Qua Ago 17, 2011 23:17
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4776 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade/Limites
 por joaofonseca » Sáb Dez 03, 2011 19:40
por joaofonseca » Sáb Dez 03, 2011 19:40
- 3 Respostas
- 2147 Exibições
- Última mensagem por LuizAquino

Sáb Dez 03, 2011 21:27
Cálculo: Limites, Derivadas e Integrais
-
- Limites e continuidade
por Marcos_Mecatronica » Sáb Abr 27, 2013 19:38
- 2 Respostas
- 1726 Exibições
- Última mensagem por e8group

Dom Abr 28, 2013 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Limites(Continuidade)
 por brunotorres123-abc » Sáb Mar 21, 2015 19:35
por brunotorres123-abc » Sáb Mar 21, 2015 19:35
- 0 Respostas
- 1752 Exibições
- Última mensagem por brunotorres123-abc

Sáb Mar 21, 2015 19:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




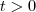 suficiente pequeno de modo que a diferença
suficiente pequeno de modo que a diferença  e o acréscimo de
e o acréscimo de  em
em  se aproxima cada vez mais de
se aproxima cada vez mais de  .Suponha que a função
.Suponha que a função 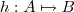 esteja definida em
esteja definida em  e
e 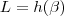 .Se
.Se  parece razoável dizer que para quaisquer números
parece razoável dizer que para quaisquer números  em
em  sempre
sempre 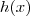 se aproxima de
se aproxima de  já que
já que  ,mas isto não necessariamente acontece ,é o caso das funções descontínuas em
,mas isto não necessariamente acontece ,é o caso das funções descontínuas em  .
. .Vamos aplicar o raciocínio (i) em seu exercício .Como
.Vamos aplicar o raciocínio (i) em seu exercício .Como ![D_f =[-3,3] D_f =[-3,3]](/latexrender/pictures/94c49f5ccf37caed6252934a0b3cb415.png) basta impor que quando
basta impor que quando 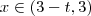 ,tem-se sempre
,tem-se sempre  ,ou seja ,
,ou seja ,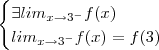 .Desta forma você obterá
.Desta forma você obterá  que satisfaça a continuidade da função no ponto 3 .Analogamente ,você achará
que satisfaça a continuidade da função no ponto 3 .Analogamente ,você achará  que satisfaça a continuidade de
que satisfaça a continuidade de  no ponto -3 ,basta impor
no ponto -3 ,basta impor  .
. 