 por samysoares » Dom Mai 26, 2013 17:13
por samysoares » Dom Mai 26, 2013 17:13
![\int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}} \int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}}](/latexrender/pictures/ab02e1099c21f28714e1f5d385c79205.png)
o resultado deveria ser:1/2ln
![\left|\sqrt[]{4{x}^{2}+9}+2x \right| \left|\sqrt[]{4{x}^{2}+9}+2x \right|](/latexrender/pictures/1d15708126a90c9cdc62789391d39666.png)
Mas o meu resutado não está bantendo: 1/2ln
![\left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right| \left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right|](/latexrender/pictures/944ba177e3545569bbae0a5d83c4563d.png)
Não sei onde estou errando, por favor me ajudem!
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Mai 26, 2013 19:36
por e8group » Dom Mai 26, 2013 19:36
Não sei o que você tentou ,mas podemos resolver esta integral por substituição trigonométrica .Observe a identidade ,
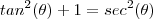
.Escrevendo o radicando

como
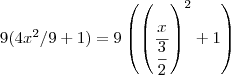
.Lembrando da identidade mencionada acima ,fica fácil ver que a substituição que vamos fazer é :

e ainda para que
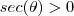
deveremos impor
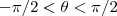
.Como
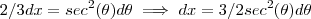
,temos que :

.
P/ resolver esta integral ,basta multiplicar em cima e em baixo por

e realizar uma nova substituição ,

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição trigonométrica.
por ClaudioSP » Qui Out 08, 2009 12:25
- 1 Respostas
- 3755 Exibições
- Última mensagem por ClaudioSP

Qui Out 08, 2009 14:25
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao trigonometrica 3
por beel » Dom Nov 27, 2011 18:24
- 3 Respostas
- 2896 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:44
Cálculo: Limites, Derivadas e Integrais
-
- integral- substituiçao trigonometrica 4
por beel » Dom Nov 27, 2011 18:29
- 1 Respostas
- 2059 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição trigonométrica
por Crist » Seg Nov 12, 2012 20:46
- 1 Respostas
- 1487 Exibições
- Última mensagem por e8group

Qui Nov 15, 2012 15:38
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição Trigonométrica
por klueger » Qua Mar 06, 2013 23:03
- 4 Respostas
- 3663 Exibições
- Última mensagem por Russman

Qui Mar 07, 2013 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}} \int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}}](/latexrender/pictures/ab02e1099c21f28714e1f5d385c79205.png)
![\left|\sqrt[]{4{x}^{2}+9}+2x \right| \left|\sqrt[]{4{x}^{2}+9}+2x \right|](/latexrender/pictures/1d15708126a90c9cdc62789391d39666.png)
![\left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right| \left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right|](/latexrender/pictures/944ba177e3545569bbae0a5d83c4563d.png)

![\int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}} \int_{}^{}\frac{dx}{\sqrt[]{4{x}^{2}+9}}](/latexrender/pictures/ab02e1099c21f28714e1f5d385c79205.png)
![\left|\sqrt[]{4{x}^{2}+9}+2x \right| \left|\sqrt[]{4{x}^{2}+9}+2x \right|](/latexrender/pictures/1d15708126a90c9cdc62789391d39666.png)
![\left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right| \left|\frac{\sqrt[]{4{x}^{2}+9}+2x}{3} \right|](/latexrender/pictures/944ba177e3545569bbae0a5d83c4563d.png)

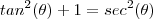 .Escrevendo o radicando
.Escrevendo o radicando  como
como 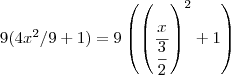 .Lembrando da identidade mencionada acima ,fica fácil ver que a substituição que vamos fazer é :
.Lembrando da identidade mencionada acima ,fica fácil ver que a substituição que vamos fazer é :  e ainda para que
e ainda para que 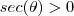 deveremos impor
deveremos impor 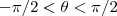 .Como
.Como 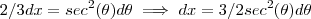 ,temos que :
,temos que :  .
. e realizar uma nova substituição ,
e realizar uma nova substituição ,  .
.