Em primeiro lugar, faz sentido integrar uma grandeza y (com relação a uma x) que não seja derivada?
Por exemplo
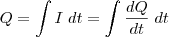
Que significa a quantidade total de carga elétrica fornecida por uma corrente elétrica dentro de um intervalo de tempo.
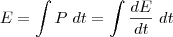
Que significa a quantidade total de energia fornecida por um equipamento dentro de dentro de um intervalo tempo.
Nos dois casos, os integrandos P e E são taxas... Não me lembro de nenhum exemplo interessante de integração que não envolva taxas...
Ademais, a razão entre duas grandezas e a derivada entre as mesmas recebem definições diferenciadas, por exemplo
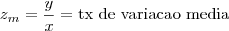
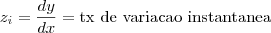
de modo que
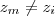
Analogamente, não existe uma definições diferentes para estes dois tipos de produto
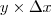e 
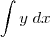? Afinal, eles também não coincidem necessariamente.E aliás, é correto definir
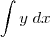como a quantidade total de unidades duma grandeza y contida no intervalo duma grandeza x. Parece boa a definição? Alguém tem algo melhor em mente?Obg!
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.