


 é racional
é racional ![\forall x \in [0,1] \forall x \in [0,1]](/latexrender/pictures/94b2e8aa70f0393b9401acc7a4fd78eb.png) então existem funções polinomiais
então existem funções polinomiais  tais que
tais que  .
.  não há nada que demonstrar . Suponhamos por absurdo que
não há nada que demonstrar . Suponhamos por absurdo que ![g(x)\neq h(x) \forall x\in (0,1] g(x)\neq h(x) \forall x\in (0,1]](/latexrender/pictures/5a9bdb70185fac78dcfe44b17c18626e.png) . Por continuidade ,
. Por continuidade , ![g(a) - h(a) = \lim_{x\to a} (g(x) - h(x)) \neq 0 \forall a \in (0,1] g(a) - h(a) = \lim_{x\to a} (g(x) - h(x)) \neq 0 \forall a \in (0,1]](/latexrender/pictures/8bdf9ae63a415cfdc9a35de9fd5b51c0.png) .
.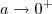 , temos que
, temos que  que é uma contradição ,pois
que é uma contradição ,pois  .
.
 para todo
para todo ![x \in [0,1] x \in [0,1]](/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) .Neste contexto ,de fato para que
.Neste contexto ,de fato para que  seja contínua e racional em
seja contínua e racional em ![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ,
,  obrigatoriamente tem que ser constante ,pois
obrigatoriamente tem que ser constante ,pois ![[0,1] [0,1]](/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) é um conjunto conexo e a imagem de conexo é conexo ,como em
é um conjunto conexo e a imagem de conexo é conexo ,como em  os conjuntos conexos são os singulares segue que a função tem que ser constante .Caso contrário , se
os conjuntos conexos são os singulares segue que a função tem que ser constante .Caso contrário , se  não fosse constante estaríamos contrariando o teorema do valor intermediário que diz
não fosse constante estaríamos contrariando o teorema do valor intermediário que diz ![f \in C([a,b]) f \in C([a,b])](/latexrender/pictures/4f7da3703af18cb00d22864c4a9ea7c9.png) e
e 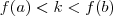 [ou
[ou 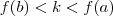 ] ,então existe
] ,então existe  tal que
tal que  . "
. "  é denso em
é denso em  ,
, 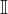 também o é .
também o é . irracional ,existe um
irracional ,existe um  em
em  tal que
tal que  que é uma contradição uma vez que
que é uma contradição uma vez que  .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes