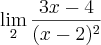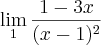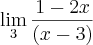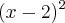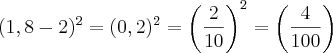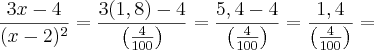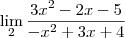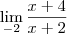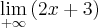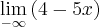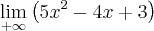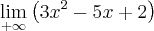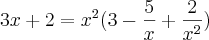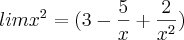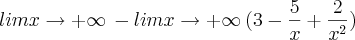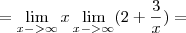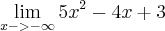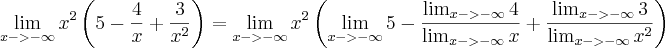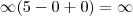[LIMITE] DUVIDA INFINITO

por **snoffao** » Qua Abr 10, 2013 14:11

Boa tarde,
Estou com duvidas nas seguintes formulas :
$\lim_{2} \frac{3x-4}{(x-2)^2}$

___
$\lim_{1} \frac{1-3x}{(x-1)^2}$

_
$\lim_{3} \frac{1-2x}{(x-3)}$

A reposta é +infinito ,-infinito e a outra é inexistente , mas eu não consigo entender e encontrar a solução! Já procurei em youtube e aqui mesmo.
Queria saber solucionar e entender o porque que é +infinito ,-infinito e a outra é inexistente ...Gostaria de saber essa diferença.

Grato

por **nakagumahissao** » Qua Abr 10, 2013 16:04

Para o primeiro limite que corresponde a mais infinito, veja como você deverá vê-lo:

-------------------->--2--<-----------------------

Imagine uma reta como mostrada acima. O sinal '>' na reta indica que iremos tomar (pegar) valores bem próximos do dois vindo da esquerda. O sinal '<' indica que iremos tomar (pegar) valores bem próximos de dois, vindo da direita.

Agora, vindo da esquerda, imagine que peguemos um valor, digamos, x = 1,8. Isto significa que o denominador:

$(x - 2)^{2}$

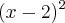
Será:

$(1,8 - 2)^{2} = (0,2)^{2} = \left(\frac{2}{10} \right)^{2} = \left(\frac{4}{100} \right)$

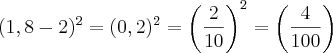
e a função toda ficará assim:

$\frac{3x - 4}{(x-2)^{2}} = \frac{3(1,8) - 4}{\left(\frac{4}{100} \right)} = \frac{5,4 - 4}{\left(\frac{4}{100} \right)} = \frac{1,4}{\left(\frac{4}{100} \right)}=$

$= 1,4 \left(\frac{100}{4} \right)$

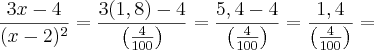
Tente agora fazer estas mesmas contas para x = 1,9, x=1,99, x = 1,9999 e você vai começar a perceber que o denominador será multiplicado por valores cada vez maiores que 100, ou seja, quanto mais nos aproximarmos de 2 pela esquerda da reta, o numerador aumentará cada vez mais, pois no limite, não estamos interessados em x = 2 e sim, em valores cada vez mais próximos de 2.

Tente também fazer estes mesmos cálculos vindo da direita de dois, ou seja, utilize x = 2,1, x= 2,01, x = 2,001, x = 2,0001 e você notará o mesmo comportamento.

Assim, conclui-se que este primeiro limite tende a 'mais infinito'.

Raciocine da mesma forma para o segundo limite apresentado e chegará a conclusão de que ele tende para 'menos infinito'

Para o terceiro, acredito que a resposta está errada. Não acredito que seja inexistente, e sim tende também à 'menos infinito'. Para que um limite não exista, os limites 'Laterais', ou seja, para este terceiro limite especificamente, o limite calculado quando se aproxima do valor 3 pela esquerda e o outro calculado quando o limite se aproxima do valor 3 pela direita deverão ser diferentes.

Espero ter ajudado.

por **snoffao** » Qui Abr 11, 2013 13:17

Eu fiquei com uma duvida. Como eu irei saber por exemplo : ' nessa questao : vou fazer a substituição, a não agora vou usar a formula tal. ' Pra saber se é infinito ou inexistente
Um exemplo :
$\lim_{2} \frac{3x-4}{(x-2)^2}$ -> resultado = infinito positivo

$\lim_{2} \frac{3x^2-2x-5}{-x^2+3x+4}$

ps: TEM UM PARENTESES GRANDE NA FORMULA TODA E O EXPOENTE É 3

RESULTADO DESSA CONTA : 1/8
__
Todas abaixo o resultado é INEXISTENTE

$\lim_{1} \frac{1}{x-1}$

$\lim_{1} \frac{1}{1-x}$

$\lim_{3} \frac{1-2x}{x-3}$

$\lim_{-2} \frac{x+4}{x+2}$

Entendeu minha duvida? Eu não estou conseguindo entender essa diferença . Como entender se ele é inexistente,+infinito e -infinito
OBS: Essas respostas foram dadas pelo professor .

por **nakagumahissao** » Qui Abr 11, 2013 13:32

snoffao,

Como foi dito já na primeira resposta:

O Limite Existe se os limites laterais existem e forem iguais. Se ao tender para um determinado valor os limites forem iguais e for crescendo indefinidamente, ele tende ao infinito. Por um outro lado, se os limites laterais forem iguais e o resultado do limite for decrescendo indefinidamente, dizemos que ele tende a 'menos' infinito. Se eles forem iguais e o resultado se aproximar de algum valor, o limite é igual à este valor. Se os limites laterais não forem iguais, ele não existe, ou seja é inexistente.

Caso tenha mais dúvidas a respeito de limites laterais, aconselho a dar uma revisada em algum livro de cálculo sobre o teorema da existência do limite por favor.

Espero que eu tenha conseguido explicar as diferenças entre 'tender' para valores (mesmo que sejam para mais ou menos infinito) e sua inexistência.

por **snoffao** » Qui Abr 11, 2013 16:30

Tem como você fazer um exemplo desses de INEXISTENTE que eu te passei, para eu tentar entender direito? :-D

por **nakagumahissao** » Sex Abr 12, 2013 01:25

Têm sim! Veja:

http://learning.freeiz.com/2013/04/12/e ... ao-existe/

[]s

por **snoffao** » Dom Abr 14, 2013 11:49

Obrigado, entendi mais ou menos.
Estou na duvida nessas questões aqui :

$\lim_{+\infty} \left(2x+3 \right)$

$\lim_{-\infty} \left(4-5x \right)$

$\lim_{+\infty} \left(5x^2-4x+3 \right)$

$\lim_{-\infty} \left(3x^3-4 \right)$

$\lim_{+\infty} \left(4-x^2 \right)$

Resposta : + infinito , + infinito ,+ infinito ,-infinito , -infinito

Agora o infinito está no lugar do numero.
O professor deu esse exemplo aqui :

$\lim_{+\infty} \left(3x^2-5x+2 \right)$
$3x+2=x^2(3-\frac{5}{x}+\frac{2}{x^2})$
$lim x^2 =(3-\frac{5}{x}+\frac{2}{x^2})$
$lim x\rightarrow+\infty \, - lim x\rightarrow+\infty \:(3-\frac{5}{x}+\frac{2}{x^2})$
$+\infty -3 = +\infty$

Tentei me guiar pra fazer os de cima nesse exercício mas não deu certo .
Tem como você me ajudar ?

Grato

por **nakagumahissao** » Dom Abr 14, 2013 13:32

Nesta primeira questão, colocamos primeiramente o x em evidência obtendo x(2 + 3/x).

$\lim_{x->\infty} 2x + 3 = \lim_{x->\infty} x(2 + \frac{3}{x})=$

$= \lim_{x->\infty} x \lim_{x->\infty} (2 + \frac{3}{x})=$

$= \lim_{x->\infty} x ( \lim_{x->\infty} 2 + \lim_{x->\infty} \frac{3}{x})= = \lim_{x->\infty} x \left( \lim_{x->\infty} 2 + \frac{\lim_{x->\infty} 3}{\lim_{x->\infty} x}\right) =$

O que fazemos agora é intuitivo. Coloquei o meu pensamento no texto abaixo, mas na realidade esta conta que fazemos não pode ser feito como mostrado. Ele foi colocado somente para que você entenda o porque do resultado ficar +Infinito. O raciocínio é o seguinte:

$= \infty (2 + 0) = \infty$

Quando x tende ao infinito, o limite de também vai para o infinito. Imagine o gráfico de y = x. y é uma reta que passa na origem e vai para +Infinito, vindo de -Infinito à medida que x cresce não é mesmo? Então se y cresce à medida que x cresce indefinidamente, então y "caminha" para +infinito. Na segunda parte temos o limite de 2 quando x tende ao infinito. Neste caso, o gráfico de y = 2 é uma reta que passa em y=2 não importando o valor de x. Ou seja, para todo x, y sempre será dois. Então mesmo que x tenda ao infinito, y sempre será 2. Logo, o limite de 2 quando x tende ao infinito será 2! - Já a última parte, lembre-se que o limite do quociente é o quociente dos limites. Esta regra você já deve ter visto antes nas aulas de cálculo. Isto ocorre sempre que o limite do denominador (a parte de baixo da fração) seja diferente de zero. Ora, o limite do denominador (limite de x quando x tende ao infinito) é diferente de zero, pois x assume valores cada vez maiores), assim o limite de 3 quando x tende ao infinito é sempre 3 no numerador; no denominador o limite de x quando x tende ao infinito é um número cada vez maior. Logo, a divisão de 3 por um número cada vez maior leva este quociente para 0. Assim, Infinito multiplicado pela soma de 2 + 0 é igual a 2 multiplicado por infinito que dá infinito, que é a nossa resposta.

O segundo item:

$\lim_{x->-\infty} 4 - 5x$

é calculado de forma similar ao primeiro. Tente fazer você por favor. Aliás, procure resolver o máximo número de exercícios possível. Se eu resolver tudo o que colocou aqui, você não vai conseguir guardar estas informações. Procure por mais exercícios no livro ou na internet para praticar, isto vai lhe ajudar muito na assimilação do conteúdo.

O terceiro item:

$\lim_{x->-\infty} 5x^{2} - 4x + 3$

No que neste caso, podemos fatorar o polinômio da seguinte maneira:

$5x^{2} - 4x + 3 = x^{2}\left(5 - \frac{4x}{x^{2}} + \frac{3}{x^{2}} \right) = x^{2}\left(5 - \frac{4}{x} + \frac{3}{x^{2}} \right)$

Agora, calculando o limite:

$\lim_{x->-\infty} x^{2}\left(5 - \frac{4}{x} + \frac{3}{x^{2}} \right) = \lim_{x->-\infty} x^{2}\left(\lim_{x->-\infty} 5 - \frac{\lim_{x->-\infty}4}{\lim_{x->-\infty} x} + \frac{\lim_{x->-\infty}3}{\lim_{x->-\infty}x^{2}} \right)$

Ora, o Limite de x ao quadrado quando x tende a menos infinito é sempre +infinito (como está elevado ao quadrado, o resultado é sempre positivo); O limite de 5 quando x tende a menos infinito é sempre 5; O limite de 4 quando x tendo a menos infinito será sempre 4; Idem para o limite de 3 quando x tende a menos infinito; O Limite de x quando x tende a menos infinito, x tomará valores tão grandes e menor que zero que 4 dividido por um número negativo gigante fará com que a fração 4/x tenda para 0; Já o limite de x ao quadrado quando x tendo para menos infinito, assumirá valores POSITIVOS tão grandes quando x tende para menos infinito que a fração 3/x ficará 0 (ZERO).

LEMBRE-SE que podemos usar a propriedade do limite do quociente PORQUE x é diferente de zero na divisão! Se fosse zero, a propriedade do limite do quociente não poderia ser aplicada. (LEMBRANDO também que o LIMITE DO QUOCIENTE é o QUOCIENTE DOS LIMITES quando o limite do denominado for diferente de zero).

Assim:

$\infty(5 - 0 + 0) = \infty$

Os outros também são similares. Tente resolver você mesmo.

Espero ter ajudado.

por **snoffao** » Dom Abr 14, 2013 17:39

Bela explicação .
Muito obrigado mesmo.

por **snoffao** » Dom Abr 14, 2013 17:39

Bela explicação .
Muito obrigado mesmo.

[LIMITE] DUVIDA INFINITO

[LIMITE] DUVIDA INFINITO

[LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Re: [LIMITE] DUVIDA INFINITO

Quem está online