Deixar comentários sobre erros e/ou acertos

por **Douglas16** » Qua Abr 03, 2013 15:19

Questão:

Seja M um ponto que divide em duas partes iguais o arco AB de uma semi-circunferência, cujo diâmetro é

.

Um raio de luz é emitido desde A e atinge a semi-circunferência num ponto Q entre M e B, e então é refletido, cruzando o diâmetro AB no ponto P.

Obtenha o valor limite do comprimento do segmento AP quando o ponto Q se aproxima infinitamente do ponto B.

Imagem

Minha resolução:
[Res.] Sendo O o centro da circunferência, sei que OP=

e ângulo OAQ= ângulo AQO= ângulo OQP.

Aplicando o teorema do seno no triângulo OQP e sabendo que , ângulo POQ= 2*(ângulo OAQ) e ângulo OPQ= pi-3*(ângulo OAQ), tenho que:

$\frac{x}{sen\left( OAQ\right)}=2a$

$x=2\cdot a \cdot sen\left(OAQ \right)$

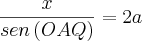
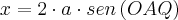
AP= $a+2 \cdot a \cdot sen\left(OAQ \right)$

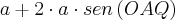
Portanto,
$\lim_{\left(OAQ \right)\rightarrow0} a+2 \cdot a \cdot sen\left(OAQ \right)=a$

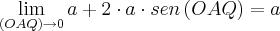
Correto ou errado?

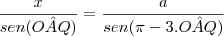
por **young_jedi** » Qua Abr 03, 2013 18:33

o angulo OPQ na verdade é

$O\^PQ=\pi-3.O\^AQ$

portanto pela relaçao do seno temos

$\frac{x}{sen(O\^AQ)}=\frac{a}{sen(\pi-3.O\^AQ)}$

$\frac{x}{sen(O\^AQ)}=\frac{a}{sen(3.O\^AQ)}$

$x=a.\frac{sen(O\^AQ)}{sen(3.O\^AQ)}$

mais o seu pensamento esta correto é este ai o camino