Dica multiplique o numerador e denominador por

, feito isto teremos a seguinte expressão :
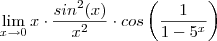
.
Através da propriedade "limite do produto é o produto dos limites " poderá argumentar que
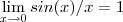
(limite trigonométrico fundamental) e que apesar de
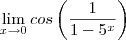
não existir (pois o mesmo está oscilando de -1 a 1 ) ,como a função cosseno é limitada , e um dos termos do produto do limite a ser calculado tende a zero quando
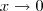
então
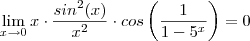
.
Outra forma de mostrar que
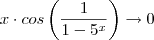
quando

é através do teorema do confronto .Para isto estabeleceremos a seguinte desigualdade que é verdadeira para todo

,
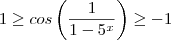
. Multiplicando membro a membro por

,
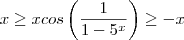
. De
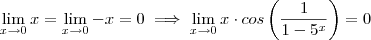
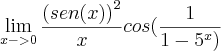 (obs:o cosseno é td a divisao) A primeira parte acredito q seja :
(obs:o cosseno é td a divisao) A primeira parte acredito q seja : 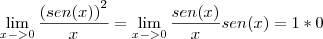 , certo?
, certo?

 , feito isto teremos a seguinte expressão :
, feito isto teremos a seguinte expressão : 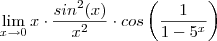 .
. 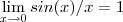 (limite trigonométrico fundamental) e que apesar de
(limite trigonométrico fundamental) e que apesar de 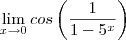 não existir (pois o mesmo está oscilando de -1 a 1 ) ,como a função cosseno é limitada , e um dos termos do produto do limite a ser calculado tende a zero quando
não existir (pois o mesmo está oscilando de -1 a 1 ) ,como a função cosseno é limitada , e um dos termos do produto do limite a ser calculado tende a zero quando 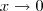 então
então 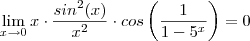 .
. 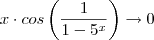 quando
quando  é através do teorema do confronto .Para isto estabeleceremos a seguinte desigualdade que é verdadeira para todo
é através do teorema do confronto .Para isto estabeleceremos a seguinte desigualdade que é verdadeira para todo  ,
, 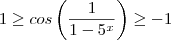 . Multiplicando membro a membro por
. Multiplicando membro a membro por 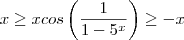 . De
. De 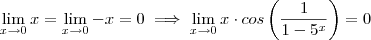


 .
.
