 por dravz » Dom Mar 24, 2013 15:17
por dravz » Dom Mar 24, 2013 15:17
Se uma bola de metal de massa m for lançada na água e a força de resistência for proporcional ao quadrado da velocidade, então a distância que a bola percorreu até o instante t é dada por:
![s(t)=m/c*ln cos h*\sqrt[2]{gc/mt} s(t)=m/c*ln cos h*\sqrt[2]{gc/mt}](/latexrender/pictures/a2351c9b573bd7633040cde4be4133c8.png)
, em que c é uma constante positiva. Encontre

.
Primeiro da ?*0, ai eu inverti o c e ficou m*c no começo da formula, mas nao to conseguindo resolver. Alguem pode dar uma ajuda?
-
dravz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 25, 2013 01:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Mar 24, 2013 16:14
por e8group » Dom Mar 24, 2013 16:14
Pergunta: a função fornecida é (1)
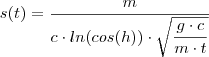
ou (2)
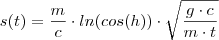
.Outra pergunta : Não seria para calcular
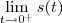
ao invés de
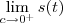
.Por favor ,confirme estas informações
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por dravz » Dom Mar 24, 2013 16:20
por dravz » Dom Mar 24, 2013 16:20
A função fornecida é a 2. E é pra calcular o limite de C->0+ mesmo.
-
dravz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 25, 2013 01:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Mar 24, 2013 18:43
por e8group » Dom Mar 24, 2013 18:43
Penso que há um erro sútil com o enunciado .
1°) Se

é constante positiva ,isto é ,

é fixo . Desta forma, não faz sentido
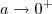
podemos sim ter

pequeno o quanto queremos, neste caso ,

.Em consequência, não podemos afirmar nada sobre o comportamento de
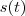
para qualquer

e sim à medida que

percorre

,pois ,

não é uma função constante e nem limitada .
2°) Há um erro em relação a expressão digitada :
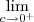
De qualquer forma ,vamos espera mais opiniões de outros usuários do ajuda matemática .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por dravz » Dom Mar 24, 2013 19:45
por dravz » Dom Mar 24, 2013 19:45
anexei o enunciado da questão pra ficar mais claro o que ta pedindo msm. nº 74!
- Anexos
-

-
dravz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 25, 2013 01:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Seg Mar 25, 2013 00:24
por e8group » Seg Mar 25, 2013 00:24
Na verdade não é
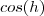
e sim cosseno hiperbólico .Neste contexto ,
![s(t) = \frac{m}{c} ln\left[cosh\left( \sqrt{\frac{g\cdot c}{m\cdot t}}\right ) \right ] = \frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] s(t) = \frac{m}{c} ln\left[cosh\left( \sqrt{\frac{g\cdot c}{m\cdot t}}\right ) \right ] = \frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ]](/latexrender/pictures/5a12edfc56319a898f8670668cd345b9.png)
,onde estamos considerando
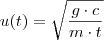
.
Observe que quando

. Assim ,
![\lim_{c\to0^+} s(t) = \lim_{u\to0^+}\frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] = \lim_{u\to0^+} \frac{g}{t} \cdot \frac{ln\dfrac{e^u + e^{-u}}{2}}{u^2} \lim_{c\to0^+} s(t) = \lim_{u\to0^+}\frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] = \lim_{u\to0^+} \frac{g}{t} \cdot \frac{ln\dfrac{e^u + e^{-u}}{2}}{u^2}](/latexrender/pictures/25ebf67edf64bd38db5b193ed23b7dec.png)
.
Este limite apresenta forma indeterminada "0/0" ,por L'hospital ,derivando o numerador e denominador com relação a
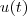
e fazendo as devidas simplificações ,vamos obter o seguinte limite equivalente ,
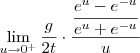
que por sua vez também apresenta indeterminação "0/0" ,portanto ,novamente por L'hospital ,segue que
![\lim_{u\to 0^+} \frac{g}{2t}\left[(e^u + e^{-u})^2 - (e^u - e^{-u})^2\right ] \lim_{u\to 0^+} \frac{g}{2t}\left[(e^u + e^{-u})^2 - (e^u - e^{-u})^2\right ]](/latexrender/pictures/6cd2eec21e2df32c3e849ceabbfe9272.png)
.
De

e
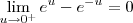
,concluímos que

.
Omitir algumas contas ,mas qualquer dúvida retorne !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por dravz » Seg Mar 25, 2013 04:19
por dravz » Seg Mar 25, 2013 04:19
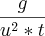
é pq vc inverteu o C, ficando m*c e depois multiplicou pela derivada da raiz ali? obrigado desde já
-
dravz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 25, 2013 01:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Seg Mar 25, 2013 11:40
por e8group » Seg Mar 25, 2013 11:40
Deixei

,certo ?
Desta expressão ,elevando ambos membros ao quadrado ,temos :
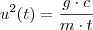
,isolando

,obtemos
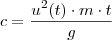
.Substituindo-se

em

,ficamos com

ou
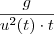
.
OBS.: Recomendo que refaça todas etapas deste execício ,daí se surgir dúvidas mande de volta !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- L'Hospital
por cal12 » Sáb Nov 26, 2011 17:52
- 1 Respostas
- 1677 Exibições
- Última mensagem por LuizAquino

Sáb Nov 26, 2011 18:13
Cálculo: Limites, Derivadas e Integrais
-
- l'hospital
por vinicastro » Dom Dez 16, 2012 16:32
- 1 Respostas
- 1514 Exibições
- Última mensagem por vinicastro

Dom Dez 16, 2012 17:15
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por matmatco » Sáb Fev 23, 2013 16:35
- 1 Respostas
- 1628 Exibições
- Última mensagem por LuizAquino

Ter Fev 26, 2013 17:09
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por duduxo81 » Sex Jul 08, 2016 11:30
- 3 Respostas
- 5264 Exibições
- Última mensagem por duduxo81

Qua Jul 13, 2016 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 20:26
- 2 Respostas
- 1914 Exibições
- Última mensagem por Claudin

Qui Jul 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![s(t)=m/c*ln cos h*\sqrt[2]{gc/mt} s(t)=m/c*ln cos h*\sqrt[2]{gc/mt}](/latexrender/pictures/a2351c9b573bd7633040cde4be4133c8.png) , em que c é uma constante positiva. Encontre
, em que c é uma constante positiva. Encontre  .
. 
![s(t)=m/c*ln cos h*\sqrt[2]{gc/mt} s(t)=m/c*ln cos h*\sqrt[2]{gc/mt}](/latexrender/pictures/a2351c9b573bd7633040cde4be4133c8.png) , em que c é uma constante positiva. Encontre
, em que c é uma constante positiva. Encontre  .
. 
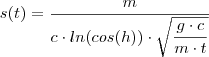 ou (2)
ou (2) 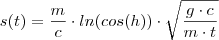 .Outra pergunta : Não seria para calcular
.Outra pergunta : Não seria para calcular 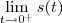 ao invés de
ao invés de 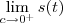 .Por favor ,confirme estas informações
.Por favor ,confirme estas informações

 é constante positiva ,isto é ,
é constante positiva ,isto é , é fixo . Desta forma, não faz sentido
é fixo . Desta forma, não faz sentido 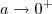 podemos sim ter
podemos sim ter  pequeno o quanto queremos, neste caso ,
pequeno o quanto queremos, neste caso , .Em consequência, não podemos afirmar nada sobre o comportamento de
.Em consequência, não podemos afirmar nada sobre o comportamento de 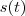 para qualquer
para qualquer  e sim à medida que
e sim à medida que  percorre
percorre  ,pois ,
,pois ,  não é uma função constante e nem limitada .
não é uma função constante e nem limitada . 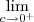


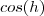 e sim cosseno hiperbólico .Neste contexto ,
e sim cosseno hiperbólico .Neste contexto , ![s(t) = \frac{m}{c} ln\left[cosh\left( \sqrt{\frac{g\cdot c}{m\cdot t}}\right ) \right ] = \frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] s(t) = \frac{m}{c} ln\left[cosh\left( \sqrt{\frac{g\cdot c}{m\cdot t}}\right ) \right ] = \frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ]](/latexrender/pictures/5a12edfc56319a898f8670668cd345b9.png) ,onde estamos considerando
,onde estamos considerando 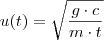 .
.  . Assim ,
. Assim , ![\lim_{c\to0^+} s(t) = \lim_{u\to0^+}\frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] = \lim_{u\to0^+} \frac{g}{t} \cdot \frac{ln\dfrac{e^u + e^{-u}}{2}}{u^2} \lim_{c\to0^+} s(t) = \lim_{u\to0^+}\frac{g}{u^2 \cdot t} \cdot ln\left[\frac{e^{u} + e^{-u}}{2} \right ] = \lim_{u\to0^+} \frac{g}{t} \cdot \frac{ln\dfrac{e^u + e^{-u}}{2}}{u^2}](/latexrender/pictures/25ebf67edf64bd38db5b193ed23b7dec.png) .
. 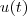 e fazendo as devidas simplificações ,vamos obter o seguinte limite equivalente ,
e fazendo as devidas simplificações ,vamos obter o seguinte limite equivalente , 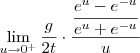 que por sua vez também apresenta indeterminação "0/0" ,portanto ,novamente por L'hospital ,segue que
que por sua vez também apresenta indeterminação "0/0" ,portanto ,novamente por L'hospital ,segue que![\lim_{u\to 0^+} \frac{g}{2t}\left[(e^u + e^{-u})^2 - (e^u - e^{-u})^2\right ] \lim_{u\to 0^+} \frac{g}{2t}\left[(e^u + e^{-u})^2 - (e^u - e^{-u})^2\right ]](/latexrender/pictures/6cd2eec21e2df32c3e849ceabbfe9272.png) .
.  e
e 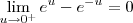 ,concluímos que
,concluímos que  .
.
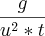 é pq vc inverteu o C, ficando m*c e depois multiplicou pela derivada da raiz ali? obrigado desde já
é pq vc inverteu o C, ficando m*c e depois multiplicou pela derivada da raiz ali? obrigado desde já
 ,certo ?
,certo ? 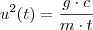 ,isolando
,isolando  ,obtemos
,obtemos 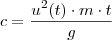 .Substituindo-se
.Substituindo-se  em
em  ,ficamos com
,ficamos com  ou
ou 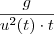 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
