![\frac{1}{4} \int_{0}^{1} 2\sqrt[]{v^{2}+8} - 2v dv](/latexrender/pictures/7df9e4a70171717c1c6c6a881dcdaec5.png "\frac{1}{4} \int_{0}^{1} 2\sqrt[]{v^{2}+8} - 2v dv")
Obrigada!
por barbara-rabello » Qua Fev 27, 2013 16:24
por Jhonata » Qua Fev 27, 2013 17:10
barbara-rabello escreveu:Não estou conseguindo resolver essa integral. É por substituição simples?
Obrigada!
![\frac{1}{4} \int_{0}^{1} 2\sqrt[]{v^{2}+8} - 2v dv = \frac{1}{2} (\int_{0}^{1} \sqrt[]{v^{2}+8} dv - \int_{0}^{1}v dv)](/latexrender/pictures/3444970fba3fd66ef4f35f666e81553e.png "\frac{1}{4} \int_{0}^{1} 2\sqrt[]{v^{2}+8} - 2v dv = \frac{1}{2} (\int_{0}^{1} \sqrt[]{v^{2}+8} dv - \int_{0}^{1}v dv)")
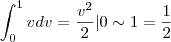
![v = 2\sqrt[]{2}tgu](/latexrender/pictures/24c6c24b035e61589db2c1e3eadaa518.png "v = 2\sqrt[]{2}tgu")
e ![dv = 2\sqrt[]{2}sec^2udu](/latexrender/pictures/f9292b61cad7b3182efccaf211acdeff.png "dv = 2\sqrt[]{2}sec^2udu")
.![\sqrt[]{x^2+8}= \sqrt[]{8tg^2u+8}](/latexrender/pictures/9b088504ccb2a996bf9ec5899f5e3f78.png "\sqrt[]{x^2+8}= \sqrt[]{8tg^2u+8}")
. Aplicando a identidade trigonométrica tg²u = sec²u - 1 substituimos, então:![\sqrt[]{8tg^2u+8} = \sqrt[]{8(sec^2x-1)+8} = 2\sqrt[]{2}secu.](/latexrender/pictures/652b9023e2ffba1b7318555dd0c9bd3f.png "\sqrt[]{8tg^2u+8} = \sqrt[]{8(sec^2x-1)+8} = 2\sqrt[]{2}secu.")
![\int_{0}^{1} \sqrt[]{v^{2}+8} dv = \int_{0}^{1}2\sqrt[]{2}sec^2u2\sqrt[]{2}secu du = 8\int_{0}^{1}sec^3u du](/latexrender/pictures/616dbf49ec4756c43f387bc3a70e6aeb.png "\int_{0}^{1} \sqrt[]{v^{2}+8} dv = \int_{0}^{1}2\sqrt[]{2}sec^2u2\sqrt[]{2}secu du = 8\int_{0}^{1}sec^3u du")
por barbara-rabello » Qua Fev 27, 2013 18:24
por Jhonata » Qui Fev 28, 2013 00:53
por Jhonata » Qui Fev 28, 2013 00:55
Jhonata escreveu:barbara-rabello escreveu:Olá!
Eu não poderia resolver a integral por substituição simples?
Por exemplo: w = v² +8
dw = 2v.
Eu tinha tentado assim, só fiquei na dúvida quanto ao sinal, pois o 2v é negativo.
Olá bárbara.
O exercício até induz a fazer isso mesmo, mas não é tão simples quanto parece. hehe.
Mas se você olhar atentamente, o "-2" é uma parcela, não um fator de multiplicação, então, particularmente, não dá pra fazer por substituição simples e acho que a forma que mostrei é a correta.
Conseguiu resolver o restante do que deixei? Espero que sim. Se você tiver o gabarito da questão, poste aí pra ver se conseguimos chegar à uma conclusão. Ou já posso postar minha resposta direto de onde parei.
Boa sorte, abraços!
por barbara-rabello » Qui Fev 28, 2013 14:07
.Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)