tenho prova de cálculo amanha e nos estudos nao consegui resolver nenhuma das integrais abaixo, se puderem me ajudar em alguma agradeco.
ps. Parece que todas se resolvem atravez de substituição trigonometrica, assunto que eu num to sabendo muito

integral sqrt(1+x^2)dx
integral {[sqrt (1+x^2)]/x^2}dx
integral {[sqrt (1+x^2)]/x^4}dx
obs.: sqrt=raiz quadrada


 , com
, com 
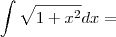
 e
e 
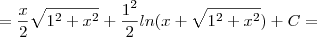




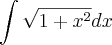
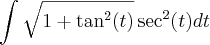
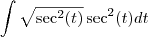

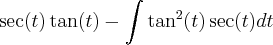


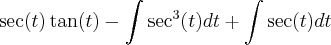
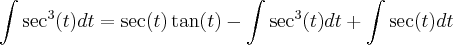
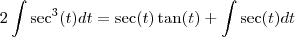
![\int\sec^3(t)dt =1/2 [\sec(t)\tan(t)] + 1/2[\int\sec(t)dt] \int\sec^3(t)dt =1/2 [\sec(t)\tan(t)] + 1/2[\int\sec(t)dt]](/latexrender/pictures/802b03dfec773e78495a96d2ba51809e.png)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.