 por solozinho » Qua Set 30, 2009 16:50
por solozinho » Qua Set 30, 2009 16:50
Boa tarde galera...
tenho prova de cálculo amanha e nos estudos nao consegui resolver nenhuma das integrais abaixo, se puderem me ajudar em alguma agradeco.
ps. Parece que todas se resolvem atravez de substituição trigonometrica, assunto que eu num to sabendo muito

integral sqrt(1+x^2)dx
integral {[sqrt (1+x^2)]/x^2}dx
integral {[sqrt (1+x^2)]/x^4}dx
obs.: sqrt=raiz quadrada
-
solozinho
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Set 30, 2009 16:34
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Eng Eletrica
- Andamento: cursando
 por Molina » Qua Set 30, 2009 18:37
por Molina » Qua Set 30, 2009 18:37
Boa tarde.
As integrais que você quer achar são do tipo

, com

O livro de cálculo que você usa deve ter uma tabela dessas integrais, basta olhar e fazer as substituições.
Vou fazer o primeiro exemplo, tente fazer o mesmo para as seguintes:
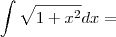
Note que da forma que definimos estas integrais, temso que

e

Pela fórmula, temos:
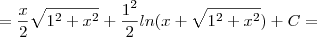

Os dois casos seguintes você considera as integrais como sendo

Então olhe a tabela de integrais e resolva essas duas.
Se encontrar dificuldades coloque-as aqui!
Boa prova amanhã
 Quando possível visite uma enquete sobre matemática e vote: viewtopic.php?f=98&t=1159
Quando possível visite uma enquete sobre matemática e vote: viewtopic.php?f=98&t=1159Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por solozinho » Qua Set 30, 2009 22:30
por solozinho » Qua Set 30, 2009 22:30
Muito obrigado Molina, a resposta é essa mesmo.
a tabela que eu uso, e que o professor deixará para consulta na prova é essa deste link:
http://www.if.ufrgs.br/tex/fisica-4/tab-integrais.pdf que nao tem essa integral.
o professor indica resolvermos por substituiçao trigonometrica...
eu comecei fazendo assim...
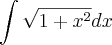
fazendo x=tg(t), dx=sec^2(t)..
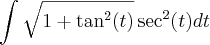
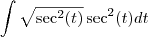

por partes, fazendo u=sec(t) => du=sec(t)tg(t)dt e dv=sec^2(t) => v=tg(t)
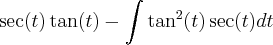


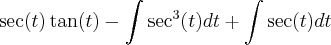
ai eu voltei à integral que estava fazendo por partes, logo...
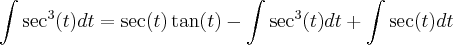
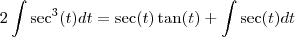
![\int\sec^3(t)dt =1/2 [\sec(t)\tan(t)] + 1/2[\int\sec(t)dt] \int\sec^3(t)dt =1/2 [\sec(t)\tan(t)] + 1/2[\int\sec(t)dt]](/latexrender/pictures/802b03dfec773e78495a96d2ba51809e.png)
e dai eu nao terminei de fazer

mas por ai ia dar certo tbm?? faltou preseverança ou ai ta tudo errado??
se tiver certo ai ja é um bom começo porque é assim que vai ser na prova

Valeu por ter ajudado ai cara..
abraço
-
solozinho
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Set 30, 2009 16:34
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Eng Eletrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral de 6/sqrt(1-x^2) no intervalo [1/2 , sqrt(3)/2]
por Costa43 » Sex Nov 01, 2013 17:29
- 2 Respostas
- 1624 Exibições
- Última mensagem por Costa43

Dom Nov 03, 2013 13:12
Cálculo: Limites, Derivadas e Integrais
-
- [Integral]sqrt(1+4x²)dx
por VenomForm » Qua Jun 19, 2013 13:57
- 1 Respostas
- 1394 Exibições
- Última mensagem por VenomForm

Qui Jun 20, 2013 11:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] SQRT 9 - (x-1)²
por Knoner » Sex Set 27, 2013 03:11
- 2 Respostas
- 1636 Exibições
- Última mensagem por Knoner

Dom Set 29, 2013 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Integrate sqrt(1-4x²) dx from 0 to 2
por VenomForm » Seg Abr 22, 2013 13:31
- 2 Respostas
- 2548 Exibições
- Última mensagem por VenomForm

Ter Abr 23, 2013 13:47
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida 1 / X SQRT (X^2 +1)
por Knoner » Qui Set 26, 2013 20:15
- 4 Respostas
- 2336 Exibições
- Última mensagem por Knoner

Sex Set 27, 2013 01:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , com
, com 
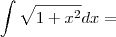
 e
e 
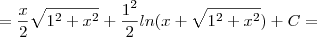




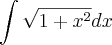
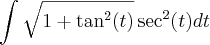
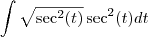

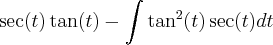


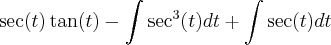
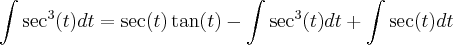
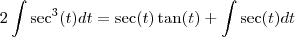
![\int\sec^3(t)dt =1/2 [\sec(t)\tan(t)] + 1/2[\int\sec(t)dt] \int\sec^3(t)dt =1/2 [\sec(t)\tan(t)] + 1/2[\int\sec(t)dt]](/latexrender/pictures/802b03dfec773e78495a96d2ba51809e.png)




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.