 por manuel_pato1 » Dom Jan 20, 2013 14:16
por manuel_pato1 » Dom Jan 20, 2013 14:16
![\int \frac{1}{\sqrt[3]{x} (\sqrt[3]{x} +1)} \int \frac{1}{\sqrt[3]{x} (\sqrt[3]{x} +1)}](/latexrender/pictures/5eb30feadef59a7cd6ab40743516fbfa.png)
dx
Bom, meu professor nos explicou de um modo que eu teria que fazer o mmc com os denominadores da função , que neste caso seria 3 , logo x= z³
então
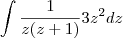
aí divido
3z² / z² + z = 3 , com um resto= -3z
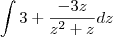
daí na segunda integral dessa última, faço por frações parciais , né?
o estranho é que se faço por frações parciais, fiz (A/z) + (B/z+1)
onde achei A= 1 e B=-1, mas a integral fica -3
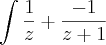
que resolvendo, resulta em -3 ln
![\left|\sqrt[3]{x} \right| \left|\sqrt[3]{x} \right|](/latexrender/pictures/1f3eed8fe0e0843f72a00d0232af61fe.png)
+ c
E 3ln
![\left|\sqrt[3]{x} +1 \right| \left|\sqrt[3]{x} +1 \right|](/latexrender/pictures/67e4e83319498a5c142a733cc57cbe0b.png)
+ c
Só que somando com a integral do começo ( 3dz ) que me resultava em 3z+c = 3
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
+ c ,
o resultado final seria :
3
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
- 3 ln
![\left|\sqrt[3]{x} \right| \left|\sqrt[3]{x} \right|](/latexrender/pictures/1f3eed8fe0e0843f72a00d0232af61fe.png)
+ 3ln
![\left|\sqrt[3]{x} +1 \right| \left|\sqrt[3]{x} +1 \right|](/latexrender/pictures/67e4e83319498a5c142a733cc57cbe0b.png)
+ c
Ou não??
o Resultado do meu professor e do wolfram foi: 3
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png)
+ 3ln
![\left|\sqrt[3]{x} +1 \right| \left|\sqrt[3]{x} +1 \right|](/latexrender/pictures/67e4e83319498a5c142a733cc57cbe0b.png)
+ c
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Dom Jan 20, 2013 20:03
por e8group » Dom Jan 20, 2013 20:03
Boa noite .
Note que ,
fazendo
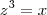
obtemos :
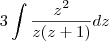
que se resume em (após cancelarmos o fator 3 no numerador e denominador)
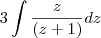
.
Somando-se
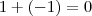
no numerador .Segue que ,

que resulta

.
Ou seja ,
![\int \frac{dx}{\sqrt[3]{x}(\sqrt[3]{x}+1)} = 3\sqrt[3]{x} - 3ln(\sqrt[3]{x} + 1) + c \int \frac{dx}{\sqrt[3]{x}(\sqrt[3]{x}+1)} = 3\sqrt[3]{x} - 3ln(\sqrt[3]{x} + 1) + c](/latexrender/pictures/fc5fa599e85d0a11ee0c6deac2411bff.png)
Por favor verifique-se o gabarito além de sua resolução .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por manuel_pato1 » Dom Jan 20, 2013 21:08
por manuel_pato1 » Dom Jan 20, 2013 21:08
Muito obrigado cara. Não tinha prestado atenção em cortar o quadrado do z que esta no numerador com o que está no numerador, e nem havia pensado sobre essa regra de somar e subtrair 1.
Pelo gabarito do meu professor, realmente está incorreto. Mas joguei no wolf e deu seu resultado mesmo.
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral de função irracional - Dúvida!
por rubenesantos » Dom Set 25, 2011 18:35
- 5 Respostas
- 6729 Exibições
- Última mensagem por rubenesantos

Sex Set 30, 2011 10:34
Cálculo: Limites, Derivadas e Integrais
-
- Integral de função com expoente irracional
por carlos_araujo » Sex Dez 05, 2014 16:54
- 1 Respostas
- 2047 Exibições
- Última mensagem por adauto martins

Qua Dez 10, 2014 15:27
Cálculo: Limites, Derivadas e Integrais
-
- Definição de função racional e irracional
por Soprano » Sex Set 30, 2016 19:52
- 0 Respostas
- 2599 Exibições
- Última mensagem por Soprano

Sex Set 30, 2016 19:52
Funções
-
- Equação Irracional
por luanxd » Ter Fev 09, 2010 23:44
- 2 Respostas
- 2078 Exibições
- Última mensagem por MarceloFantini

Qua Fev 10, 2010 12:38
Sistemas de Equações
-
- Eguação Irracional
por rhodry » Dom Nov 27, 2011 15:27
- 13 Respostas
- 7017 Exibições
- Última mensagem por vcbuldrini

Qui Dez 01, 2011 19:53
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int \frac{1}{\sqrt[3]{x} (\sqrt[3]{x} +1)} \int \frac{1}{\sqrt[3]{x} (\sqrt[3]{x} +1)}](/latexrender/pictures/5eb30feadef59a7cd6ab40743516fbfa.png) dx
dx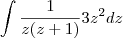
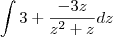
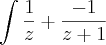
![\left|\sqrt[3]{x} \right| \left|\sqrt[3]{x} \right|](/latexrender/pictures/1f3eed8fe0e0843f72a00d0232af61fe.png) + c E 3ln
+ c E 3ln![\left|\sqrt[3]{x} +1 \right| \left|\sqrt[3]{x} +1 \right|](/latexrender/pictures/67e4e83319498a5c142a733cc57cbe0b.png) + c
+ c ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) + c ,
+ c , ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) - 3 ln
- 3 ln![\left|\sqrt[3]{x} \right| \left|\sqrt[3]{x} \right|](/latexrender/pictures/1f3eed8fe0e0843f72a00d0232af61fe.png) + 3ln
+ 3ln![\left|\sqrt[3]{x} +1 \right| \left|\sqrt[3]{x} +1 \right|](/latexrender/pictures/67e4e83319498a5c142a733cc57cbe0b.png) + c
+ c ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) + 3ln
+ 3ln![\left|\sqrt[3]{x} +1 \right| \left|\sqrt[3]{x} +1 \right|](/latexrender/pictures/67e4e83319498a5c142a733cc57cbe0b.png) + c
+ c

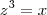 obtemos :
obtemos :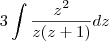 que se resume em (após cancelarmos o fator 3 no numerador e denominador)
que se resume em (após cancelarmos o fator 3 no numerador e denominador) 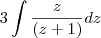 .
. 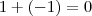 no numerador .Segue que ,
no numerador .Segue que , que resulta
que resulta  .
. ![\int \frac{dx}{\sqrt[3]{x}(\sqrt[3]{x}+1)} = 3\sqrt[3]{x} - 3ln(\sqrt[3]{x} + 1) + c \int \frac{dx}{\sqrt[3]{x}(\sqrt[3]{x}+1)} = 3\sqrt[3]{x} - 3ln(\sqrt[3]{x} + 1) + c](/latexrender/pictures/fc5fa599e85d0a11ee0c6deac2411bff.png)






