Boa noite .
Vamos trabalhar no numerador .
A seguir vamos utilizar algumas propriedades ,dentre elas comutatividade,distributividade, e do elemento neutro da soma .
Ressaltando que , (sendo a,b,c números reais )
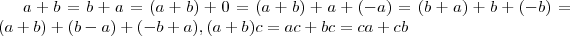
.
Então ,

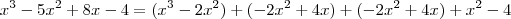
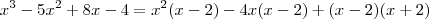
![x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2] x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2]](/latexrender/pictures/f5dab17557e2830a21abec2daac3f8ea.png)
Quanto o denominador pode dividir ele por

ou fazer o mesmo método acima .Deixo como exercício para você .
Feito isto você , poderá simplificar o termo

que aparecerá no númerador e no denominador . Note que isto só é possível pois
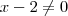
para
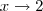
.
OBS.: Evite escrever desta forma ,recomendo que utilize os parênteses ( ) . Perceba que (a+b)/c = a/c + b/c .Já a+b/c , fica subtendido-se que é b/c + a . A segunda opção seria utilizar o comando \frac{a+b}{c} cujo resultado é
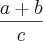
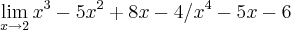


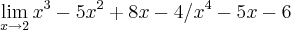

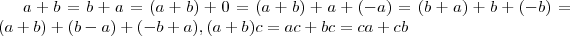 .
. 
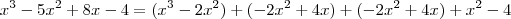
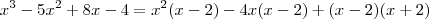
![x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2] x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2]](/latexrender/pictures/f5dab17557e2830a21abec2daac3f8ea.png)
 ou fazer o mesmo método acima .Deixo como exercício para você .
ou fazer o mesmo método acima .Deixo como exercício para você .  que aparecerá no númerador e no denominador . Note que isto só é possível pois
que aparecerá no númerador e no denominador . Note que isto só é possível pois 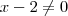 para
para 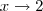 .
.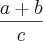



 .
.
 :
: