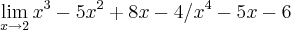


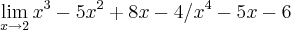

 .
. 
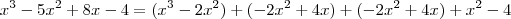
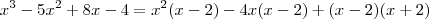
![x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2] x^3 -5x^2 + 8x - 4 = (x-2)[x^2 - 4x + x + 2]](/latexrender/pictures/f5dab17557e2830a21abec2daac3f8ea.png)
 ou fazer o mesmo método acima .Deixo como exercício para você .
ou fazer o mesmo método acima .Deixo como exercício para você .  que aparecerá no númerador e no denominador . Note que isto só é possível pois
que aparecerá no númerador e no denominador . Note que isto só é possível pois 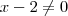 para
para 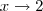 .
.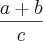


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

