![f(x)=\frac{{x}^{3}}{\sqrt[]{2-{x}^{2}}} f(x)=\frac{{x}^{3}}{\sqrt[]{2-{x}^{2}}}](/latexrender/pictures/9f430f37b0aaab0a6f8061c90ec0a13c.png) utilizando o metodo de substituiçao?
utilizando o metodo de substituiçao?

![f(x)=\frac{{x}^{3}}{\sqrt[]{2-{x}^{2}}} f(x)=\frac{{x}^{3}}{\sqrt[]{2-{x}^{2}}}](/latexrender/pictures/9f430f37b0aaab0a6f8061c90ec0a13c.png) utilizando o metodo de substituiçao?
utilizando o metodo de substituiçao?
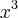 .
.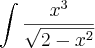 =
= 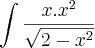
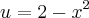 e
e 
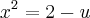 e
e 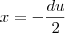


![\int_{}^{}\frac{\frac{-du}{2}.(2-u)}{\sqrt[]{u}}.du \int_{}^{}\frac{\frac{-du}{2}.(2-u)}{\sqrt[]{u}}.du](/latexrender/pictures/aa2c4a2b58507cae9246db9e44996bc4.png)
![\frac{1}{2}\int_{}^{}du.\frac{1}{\sqrt[]{u}}(2u).du = \frac{1}{2}\int_{}^{}du.\frac{1}{\sqrt[]{u}}(2-u).du = \frac{1}{2}ln\left|\sqrt[]{u} \right|.\int_{}^{}du(2-u).du \frac{1}{2}\int_{}^{}du.\frac{1}{\sqrt[]{u}}(2u).du = \frac{1}{2}\int_{}^{}du.\frac{1}{\sqrt[]{u}}(2-u).du = \frac{1}{2}ln\left|\sqrt[]{u} \right|.\int_{}^{}du(2-u).du](/latexrender/pictures/6fe7fc603096652d513ad6eecc91d842.png) ?
?
![x^3 = -x (-x^2) = -x(-x^2 + (-2)+2)) = -x(2 - x^2 -2) = \\
\quad = \quad-x([\sqrt{2-x^2}]^2 - 2) = -x(\sqrt{2-x^2}\cdot \sqrt{2-x^2} - 2) = \\
\quad = \quad -[\sqrt{2-x^2}\cdot\sqrt{2-x^2}]\cdot x + 2x x^3 = -x (-x^2) = -x(-x^2 + (-2)+2)) = -x(2 - x^2 -2) = \\
\quad = \quad-x([\sqrt{2-x^2}]^2 - 2) = -x(\sqrt{2-x^2}\cdot \sqrt{2-x^2} - 2) = \\
\quad = \quad -[\sqrt{2-x^2}\cdot\sqrt{2-x^2}]\cdot x + 2x](/latexrender/pictures/56831338490920214242554ab50af9a4.png) .
. .Elemento neutro da soma .
.Elemento neutro da soma . 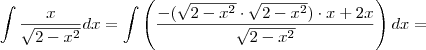
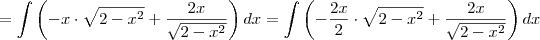
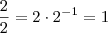 .Elemento neutro da multiplicação
.Elemento neutro da multiplicação 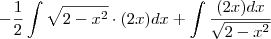 .
. 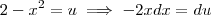 .
. 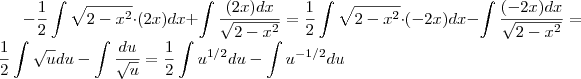 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)