Questão: Encontre a derivada da função abaixo:
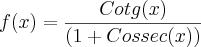
Resolução:
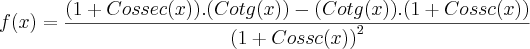

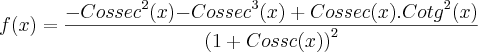




- Aplico que: se
 então
então  ;
;
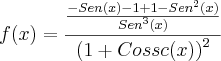
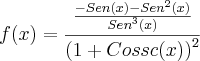
Dúvida:
- Parei por aqui. Não sei "da onde" que isso vai chegar na resposta que consta no gabarito do livro do Anton.
- E outra: Depois de se aplicar a regra de derivada de um quociente, o resultado não poderia ser a resposta? Porque, a mim me parece que estas derivadas trigonométricas tem respostas um tanto quanto subjetivas, digo, dependendo do caminho - identidades trigonométricas aplicadas - que você toma chega-se a diferentes resoluções. Isso é normal?
Gabarito:
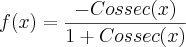




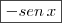 .
. e nós tivéssemos encontrado
e nós tivéssemos encontrado  , ou até mesmo
, ou até mesmo 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)