tentei resolver usando teorema do confronto, mas não deu muito certo..
fiz que 0 < ou = | x² / (sqrt(x² + y²)) | = x² / (sqrt(x² + y²)) < ou igual (não consegui essa parte do confronto)
me ajudem?

obrigado!!



 , de modo que
, de modo que 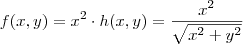 .
. 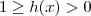 . Multiplicando toda desigualdade por
. Multiplicando toda desigualdade por  temos que ,
temos que , 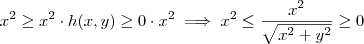 .
. 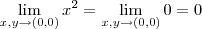
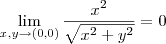 .
.
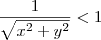 .Tome por exemplo
.Tome por exemplo  e
e 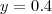 .
.  , para
, para  em uma vizinhança do zero , de forma que
em uma vizinhança do zero , de forma que 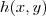 seja estritamente maior que zero e menor que
seja estritamente maior que zero e menor que  .
.  que implica
que implica 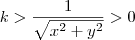 .Multiplicando toda inequação por
.Multiplicando toda inequação por  temos ,
temos ,  .
. 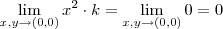
 .
. 

 apenas para
apenas para  em uma vizinhança do zero , isto é quando
em uma vizinhança do zero , isto é quando  .
. 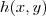 .
. 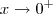 . Vamos pegar valores testes , como por exemplo :
. Vamos pegar valores testes , como por exemplo :  .
. 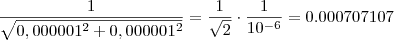 .
.  . Pela nossa hipótese ,existe um
. Pela nossa hipótese ,existe um 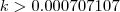 quando
quando 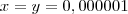 .
.  .
. 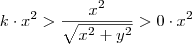 .
.  novamente . Vamos , ter :
novamente . Vamos , ter :  .
. 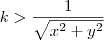 . Façamos então ,
. Façamos então , 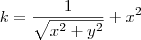 , é obvio que
, é obvio que  .
. 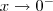 .
. 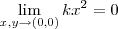 e
e  . Vamos ver que os demais usuarios do ajuda matmática acham .
. Vamos ver que os demais usuarios do ajuda matmática acham . 

inkz escreveu:agora ficou mais claro, e pude entender!!
parece razoável que seja realmente uma solução válida.
mas será que a que sugeri, de usar o teo de função limitada daria certo?
obrigado!!
inkz escreveu:
mas será que a que sugeri, de usar o teo de função limitada daria certo?
 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)