
1) Esboce a trajetória da curva gama(t) = ( e^t, e^(2t) )
como fiz:
x=e^t
y=e^2t
y=(e^t)^2 = x^2
então, a trajetória da curva gama(t) está contida na parábola y=x², porém apenas no primeiro quadrante, já que a imagem de gama(t) é maior ou igual a zero, para qualquer (t) pertencente ao seu domínio...
é isso mesmo?
valeeu =]


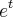 é maior que zero. Lembre-se que a exponencial nunca se anula e é sempre positiva.
é maior que zero. Lembre-se que a exponencial nunca se anula e é sempre positiva. , ou seja, a parábola chega arbitrariamente próximo de zero, mas nunca é zero, e vai para infinito.
, ou seja, a parábola chega arbitrariamente próximo de zero, mas nunca é zero, e vai para infinito.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)