 por Gustavo Gomes » Qui Nov 08, 2012 21:41
por Gustavo Gomes » Qui Nov 08, 2012 21:41
Pessoal, como posso provar que
![f(x)=\sqrt[n]{x} f(x)=\sqrt[n]{x}](/latexrender/pictures/cfbdca0f166ffba183cb554ce1beaeea.png)
é contínua?
Pensei em analisar separadamente para n par e n impar. (n>0)
Para n par:
Sendo
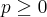
e Tomando
![\epsilon>0, \epsilon<\sqrt[n]{x} \epsilon>0, \epsilon<\sqrt[n]{x}](/latexrender/pictures/127519c8ceb387b4b37b0a02b0c3b70c.png)
:
![\sqrt[n]{p}-\epsilon<\sqrt[n]{x}<\sqrt[n]{p}+\epsilon \sqrt[n]{p}-\epsilon<\sqrt[n]{x}<\sqrt[n]{p}+\epsilon](/latexrender/pictures/23122597e735d7217c49deb04bd86e0e.png)
.
Daí não consegui prosseguir e encontrar um intervalo I do domínio que garanta a continuidade para todo n em questão.....
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por MarceloFantini » Qui Nov 08, 2012 22:40
por MarceloFantini » Qui Nov 08, 2012 22:40
Algumas coisas:

é inteiro ou não? Caso contrário, sua afirmação sobre ser par não faz sentido.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Gustavo Gomes » Sex Nov 09, 2012 21:33
por Gustavo Gomes » Sex Nov 09, 2012 21:33
Para n natural, Marcelo.
Grato.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstração continuidade de uma função diferenciável
por Beatriz4 » Sáb Abr 28, 2012 20:58
- 1 Respostas
- 1649 Exibições
- Última mensagem por fraol

Ter Mai 01, 2012 01:40
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade] Demonstração
por Aliocha Karamazov » Sáb Out 29, 2011 14:20
- 4 Respostas
- 3121 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Out 29, 2011 21:11
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade de função
por marinalcd » Qui Ago 23, 2012 20:52
- 0 Respostas
- 1044 Exibições
- Última mensagem por marinalcd

Qui Ago 23, 2012 20:52
Funções
-
- continuidade da função
por Sherminator » Sex Nov 16, 2012 13:13
- 15 Respostas
- 12127 Exibições
- Última mensagem por Sherminator

Ter Nov 20, 2012 12:55
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade da função
por Lenin » Qua Set 25, 2013 21:21
- 1 Respostas
- 1365 Exibições
- Última mensagem por Man Utd

Qua Set 25, 2013 21:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=\sqrt[n]{x} f(x)=\sqrt[n]{x}](/latexrender/pictures/cfbdca0f166ffba183cb554ce1beaeea.png) é contínua?
é contínua?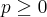 e Tomando
e Tomando ![\epsilon>0, \epsilon<\sqrt[n]{x} \epsilon>0, \epsilon<\sqrt[n]{x}](/latexrender/pictures/127519c8ceb387b4b37b0a02b0c3b70c.png) :
:![\sqrt[n]{p}-\epsilon<\sqrt[n]{x}<\sqrt[n]{p}+\epsilon \sqrt[n]{p}-\epsilon<\sqrt[n]{x}<\sqrt[n]{p}+\epsilon](/latexrender/pictures/23122597e735d7217c49deb04bd86e0e.png) .
.
![f(x)=\sqrt[n]{x} f(x)=\sqrt[n]{x}](/latexrender/pictures/cfbdca0f166ffba183cb554ce1beaeea.png) é contínua?
é contínua?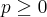 e Tomando
e Tomando ![\epsilon>0, \epsilon<\sqrt[n]{x} \epsilon>0, \epsilon<\sqrt[n]{x}](/latexrender/pictures/127519c8ceb387b4b37b0a02b0c3b70c.png) :
:![\sqrt[n]{p}-\epsilon<\sqrt[n]{x}<\sqrt[n]{p}+\epsilon \sqrt[n]{p}-\epsilon<\sqrt[n]{x}<\sqrt[n]{p}+\epsilon](/latexrender/pictures/23122597e735d7217c49deb04bd86e0e.png) .
.
 é inteiro ou não? Caso contrário, sua afirmação sobre ser par não faz sentido.
é inteiro ou não? Caso contrário, sua afirmação sobre ser par não faz sentido.



 .
.



