Seja
 , l > 0
, l > 0a) Calcule a diferencial.
b) Interprete geometricamente o erro que se comete na aproximação de
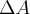 por dA. (Olhe para
por dA. (Olhe para  como a fórmula para o cálculo da área de quadrado de lado L).
como a fórmula para o cálculo da área de quadrado de lado L).a)
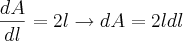
Estou com duvida na hora de encontra o erro quando
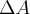 aproxima de dA,tpw usando a formula de
aproxima de dA,tpw usando a formula de 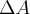
eu chego em

 +
+ ^2
^2mais i ai q interpretaçao devo ter,por favor me ajudem nesse assunto de erro


 e que
e que  . Você também sabe que por definição temos
. Você também sabe que por definição temos  . Portanto, temos que
. Portanto, temos que  . Comparando então
. Comparando então  (ou
(ou 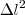 , já que
, já que 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)