Faço uma troca de variaveis com e elevado a 2x -1 e depois aplico logaritmo neperiano, mass não chego no resultado.




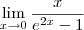 . Aplicando as mesmas ideias exibidas nessa solução você resolverá o limite desejado.
. Aplicando as mesmas ideias exibidas nessa solução você resolverá o limite desejado.
![\lim_{x\rightarrow{0}}]\frac{\epsilon^{x^2}-1}{x} \lim_{x\rightarrow{0}}]\frac{\epsilon^{x^2}-1}{x}](/latexrender/pictures/558397f2417e81aa5df1249ec3700b11.png)

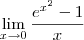
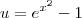 . Quando x tende para zero, temos que u também tende para zero.
. Quando x tende para zero, temos que u também tende para zero. . Nesse ponto, há um detalhe importante. Quando u se aproxima de zero pela esquerda, sabemos que
. Nesse ponto, há um detalhe importante. Quando u se aproxima de zero pela esquerda, sabemos que  . Por isso, simplesmente escrever
. Por isso, simplesmente escrever  é um erro.
é um erro.
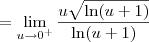


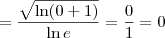
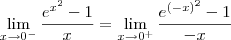
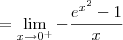
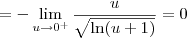
 , podemos afirmar que
, podemos afirmar que  .
.


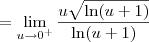


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.
 :
: