 por menino de ouro » Qua Out 24, 2012 16:12
por menino de ouro » Qua Out 24, 2012 16:12
por favor me ajude a resolver e entender essa questão de integral por substituição simples:
a)

usando uma dessas formulas:
![\int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a \int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a](/latexrender/pictures/3e4b8a829a8d58b4862603fa6f520676.png)
![\int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a \int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a](/latexrender/pictures/d02a16b28a08e1be2a3a52797edc0676.png)

eu estou começando a aprender a substituição de uma variável (x) por u.du ( du = a derivada de u)
ou seja escolhendo um termo da fraçao que contenha (x )no denominador ou no numerador.
estou com bastante dificuldade pois meu curso é a distancia (EAD) e ?o tem o professor ,não tem tutor!pois são poucos alunos e a maioria já passou nesta disciplina(calculo 2) ou desistiu do curso
obrigado!
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por young_jedi » Qua Out 24, 2012 16:51
por young_jedi » Qua Out 24, 2012 16:51
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TECNICAS DE INTEGRAÇÃO
por Marcio Cristo » Qui Dez 22, 2011 18:35
- 5 Respostas
- 3020 Exibições
- Última mensagem por LuizAquino

Sex Dez 23, 2011 18:00
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração
por Victor Mello » Seg Nov 18, 2013 23:04
- 2 Respostas
- 1642 Exibições
- Última mensagem por Victor Mello

Ter Nov 19, 2013 00:16
Cálculo: Limites, Derivadas e Integrais
-
- [tecnicas de integraçao por partes (u)(dv)]
por menino de ouro » Ter Out 30, 2012 18:21
- 3 Respostas
- 2069 Exibições
- Última mensagem por MarceloFantini

Ter Out 30, 2012 22:39
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração - multiplicando pelo fator unitário
por Victor Mello » Qui Nov 21, 2013 18:37
- 2 Respostas
- 1705 Exibições
- Última mensagem por Victor Mello

Qui Nov 21, 2013 23:27
Cálculo: Limites, Derivadas e Integrais
-
- [Usando tecnicas de integrais por substituiçao simples]
por menino de ouro » Qua Out 24, 2012 23:10
- 1 Respostas
- 1681 Exibições
- Última mensagem por MarceloFantini

Qui Out 25, 2012 01:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a \int \frac{1}{\sqrt[]{a^2 -x^2}}dx =arcsen \frac{x}{a} +c,\left|x \right|<a](/latexrender/pictures/3e4b8a829a8d58b4862603fa6f520676.png)
![\int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a \int \frac{1}{x \sqrt[]{x^2 -a^2}}dx =\frac{1}{a}arcsec \left|\frac{x}{a} \right| +c,\left|x \right|>a](/latexrender/pictures/d02a16b28a08e1be2a3a52797edc0676.png)



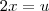





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.